练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知曲线C1:y=x2与曲线C2:y=-(x-2)2,直线l与C1和C2都相切,求直线l的方程.

    【答案】或

    【解析】

    先设出直线与两曲线的切点坐标P(x1,)和Q(x2,-(x2-2)2)，根据导数的几何意义分别求出切线的方程，再根据两切线重合得到关于和的方程组，求得和后可得切线方程．

    设l与C1相切于点P(x1,),与C2相切于点Q(x2,-(x2-2)2).

    对于曲线C1，有y'=2x，

    所以与C1相切于点P的切线方程为y-=2x1(x-x1)，

    即y=2x1x．①

    对于曲线C2，有y'=-2(x-2),

    所以与C2相切于点Q的切线方程为y+(x2-2)2=-2(x2-2)(x-x2),

    即y=-2(x2-2)x+．②

    由题意得两切线重合，

    所以由①②得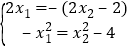，解得或．

    所以直线l的方程为或．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的离心率为 ，左右焦点分别为F1 ， F2 ， 以椭圆短轴为直径的圆与直线 相切．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）过点F1、斜率为k1的直线l1与椭圆E交于A，B两点，过点F2、斜率为k2的直线l2与椭圆E交于C，D两点，且直线l1 ， l2相交于点P，若直线OA，OB，OC，OD的斜率kOA ， kOB ， kOC ， kOD满足kOA+kOB=kOC+kOD ， 求证：动点P在定椭圆上，并求出此椭圆方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大学为调查来自南方和北方的同龄大学生的身高差异，从2016级的年龄在18～19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名，测量他们的身高，量出的身高如下(单位：cm)：

    南方：158，170，166，169，180，175，171，176，162，163.

    北方：183，173，169，163，179，171，157，175，184，166.

    (1)根据抽测结果，画出茎叶图，对来自南方和北方的大学生的身高作比较，写出统计结论．

    (2)设抽测的10名南方大学生的平均身高为x cm，将10名南方大学生的身高依次输入如图所示的程序框图进行运算，问输出的s大小为多少？并说明s的统计学意义．

    (3)为进一步调查身高与生活习惯的关系，现从来自南方的这10名大学生中随机抽取2名身高不低于170 cm的学生，求身高为176 cm的学生被抽中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且满足向量 =（cosA，cosB）， =（a，2c﹣b）， ∥ ．
    （1）求角A的大小；
    （2）若a=2 ，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中，真命题是（ ）
    A.x∈R，2x＞x2
    B.若a＞b，c＞d，则 a﹣c＞b﹣d
    C.x∈R，ex＜0
    D.ac2＜bc2是a＜b的充分不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（1，2）， =（﹣2，m）， = +（t2+1） ， =﹣k + ，m∈R，k、t为正实数．
    （1）若 ∥ ，求m的值；
    （2）若 ⊥ ，求m的值；
    （3）当m=1时，若 ⊥ ，求k的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】冶炼某种金属可以用旧设备和改造后的新设备，为了检验用这两种设备生产的产品中所含杂质的关系，调查结果如下表所示：

    分类

    杂质高

    杂质低

    旧设备

    37

    121

    新设备

    22

    202

    根据以上数据，则(　　)

    A. 含杂质的高低与设备改造有关

    B. 含杂质的高低与设备改造无关

    C. 设备是否改造决定含杂质的高低

    D. 以上答案都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，椭圆C： =1（a＞1）的左、右顶点分别为A、B，P是椭圆C上任一点，且点P位于第一象限．直线PA交y轴于点Q，直线PB交y轴于点R．当点Q坐标为（0，1）时，点R坐标为（0，2）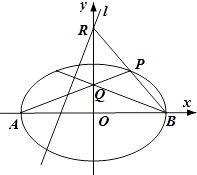

    （1）求椭圆C的标准方程；
    （2）求证： 为定值；
    （3）求证：过点R且与直线QB垂直的直线经过定点，并求出该定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知M,N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,线段MN的中点A的横坐标为.

    (1)求|MF|+|NF|的值;

    (2)若p=2,直线MN与x轴交于点B,求点B的横坐标的取值范围.

    查看答案和解析>>

    同步练习册答案