解:(1)因为
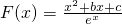
,所以
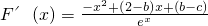
,
又因为F(x)图象在x=0处的切线方程为x-y=0,
所以
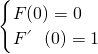
,即
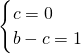
,解得 b=1,c=0.
(2)①因为F(x)是(-∞,+∞)上的单调递减函数,所以F′(x)≤0恒成立,
即-x
2+(2-b)x+(b-c)≤0对任意的x∈R恒成立,
所以△=(2-b)
2+4(b-c)≤0,所以
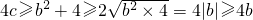
,即c>b且c≥1,
令g(x)=f(x)-(x+c)
2=(b-2c)x-c(c-1),由b-2c<0,知g(x)是减函数,
故g(x)在[0,+∞)内取得最小值g(0),又g(0)=-c(c-1)≤0,
所以x≥0时,g(x)≤g(0)≤0,即f(x)≤(x+c)
2.
②由①知,c≥|b|≥0,当|b|=c时,b=c或b=-c,
因为b
2+4-4c≤0,即c
2+4-4c≤0,解得c=2,b=2或b=-2,所以f(x)=x
2±2x+2,
而f(c)-f(b)=c
2+bc+c-b
2-b
2-c=c
2+bc-2b
2=(c+2b)(c-b),
所以f(c)-f(b)=-8或0,
不等式f(c)-Mc
2≤f(b)-Mb
2等价于f(c)-f(b)≤M(c
2-b
2),
变为-8≤M•0或0≤M•0恒成立,M∈R,
当|b|≠c时,c>|b|,即c
2-b
2>0,所以不等式f(c)-Mc
2≤f(b)-Mb
2恒成立等价于

恒成立,等价于

,
而
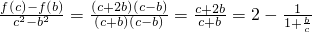
,
因为c>|b|,
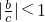
,所以
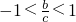
,所以

,所以

,
所以
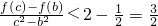
,所以
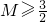
.
分析:(1)欲求b,c的值,根据所给的切线方程,只须求出切线斜率即可,故先利用导数求出在x=0处的导函数值,再结合导数的几何意义即可求出切线的斜率进而得切线方程,最后与所给的方程比较即得b,c的值;
(2)根据函数F(x)是(-∞,+∞)上单调递减,得到F′(x)≤0恒成立,从而得到c>b且c≥1,①令g(x)=f(x)-(x+c)
2=(b-2c)x-c(c-1),从而得到结果;
②不等式f(c)-Mc
2≤f(b)-Mb
2恒成立等价于f(c)-f(b)≤M(c
2-b
2)恒成立,分离参数可得

恒成立,转化为求
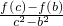
的最大值即可.
点评:本小题主要考查利用导数研究函数的极单调性、导数的几何意义、利用导数研究曲线上某点切线方程,考查学生灵活应用知识分析解决问题的能力和运算求解能力,体现了转化的数学思想方法.属难题.

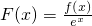 ,
,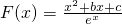 ,所以
,所以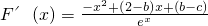 ,
,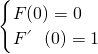 ,即
,即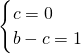 ,解得 b=1,c=0.
,解得 b=1,c=0.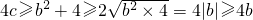 ,即c>b且c≥1,
,即c>b且c≥1, 恒成立,等价于
恒成立,等价于 ,
,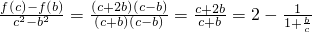 ,
,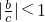 ,所以
,所以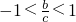 ,所以
,所以 ,所以
,所以 ,
,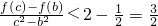 ,所以
,所以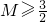 .
. 恒成立,转化为求
恒成立,转化为求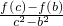 的最大值即可.
的最大值即可.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<