
(本小题满分14分)已知函数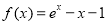 ,
, , 其中,
, 其中,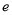 是自然对数的底数.函数
是自然对数的底数.函数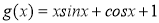 ,
, .
.
(Ⅰ)求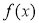 的最小值;
的最小值;
(Ⅱ)将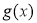 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列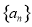 ,求证:
,求证:
(1)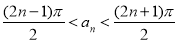 ,其中
,其中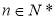 ;
;
(2)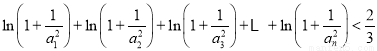 .
.
(Ⅰ)0(Ⅱ)证明见解析
【解析】
试题分析:(1)解决类似的问题时,注意区分函数的最值和极值.求函数的最值时,要先求函数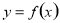 在区间
在区间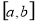 内使
内使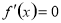 的点,再计算函数
的点,再计算函数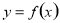 在区间内所有使
在区间内所有使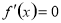 的点和区间端点处的函数值,最后比较即得;(2)证明不等式,利用函数的单调性很常见,一定要注意选取恰当的函数及单调区间(3)不等式具有放缩功能,常常用于证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好切入点.
的点和区间端点处的函数值,最后比较即得;(2)证明不等式,利用函数的单调性很常见,一定要注意选取恰当的函数及单调区间(3)不等式具有放缩功能,常常用于证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好切入点.
试题解析:(Ⅰ)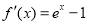 ,当
,当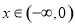 时,
时,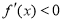 ;当
;当 时,
时,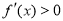 ;所以,函数
;所以,函数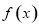 在
在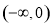 上是减函数,在
上是减函数,在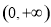 上是增函数,所以
上是增函数,所以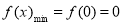 ,
,
综上所述,函数 的最小值是0. 4分
的最小值是0. 4分
(Ⅱ)证明:对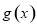 求导得
求导得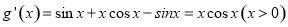 ,令
,令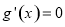 可得
可得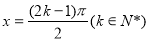 ,当
,当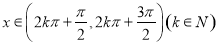 时,
时,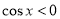 ,此时
,此时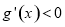 ;当
;当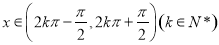 时,
时,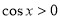 ,此时
,此时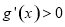 .所以,函数
.所以,函数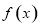 的单调递减区间为
的单调递减区间为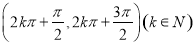 ,单调递增区间为
,单调递增区间为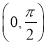 和
和 . 7分
. 7分
因为函数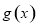 在区间
在区间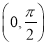 上单调递增,又
上单调递增,又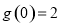 ,所以
,所以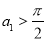 .当
.当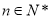 时,因为
时,因为 ,且函数
,且函数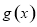 的图像是连续不断的,所以
的图像是连续不断的,所以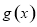 在区间
在区间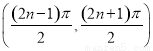 内至少存在一个零点,又
内至少存在一个零点,又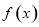 在区间
在区间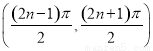 上是单调的,故
上是单调的,故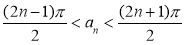 . 9分
. 9分
(2)证明:由(Ⅰ)知,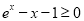 ,则
,则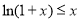 ,因此,当
,因此,当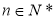 时,
时,
记S=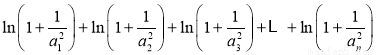
则S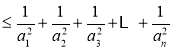 11分
11分
由(1)知,S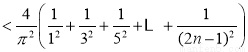
当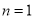 时,
时, ;
;
当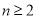 时,S
时,S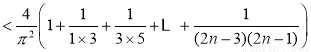
即,S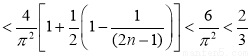 ,证毕. 14分
,证毕. 14分
考点:利用导数求函数最值,利用单调性及放缩法证明不等式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年山东省文登市高三上学期第一次考试理科数学试卷(解析版) 题型:选择题
已知函数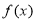 是奇函数,当
是奇函数,当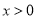 时,
时, ,且
,且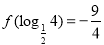 ,则
,则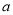 的值为( )
的值为( )
A.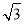 B.
B.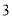 C.
C.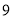 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省济宁市高三上学期期中考试文科数学试卷(解析版) 题型:选择题
在正项等比数列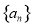 中,
中,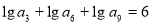 ,则
,则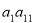 的值是 ( )
的值是 ( )
(A)10000 (B)1000 (C)100 (D)10
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省襄阳市高三上学期11月质检文科数学试卷(解析版) 题型:填空题
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图所示的三角形数:

将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn},可以推测:(Ⅰ)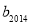 是数列
是数列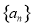 中的第_________项;(Ⅱ)若
中的第_________项;(Ⅱ)若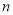 为正偶数,则
为正偶数,则 =_________.(用n表示)
=_________.(用n表示)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省襄阳市高三上学期11月质检文科数学试卷(解析版) 题型:选择题
已知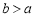 ,若函数
,若函数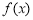 在定义域内的一个区间
在定义域内的一个区间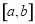 上函数值的取值范围恰好是
上函数值的取值范围恰好是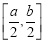 ,则称区间
,则称区间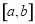 是函数
是函数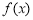 的一个减半压缩区间,若函数
的一个减半压缩区间,若函数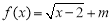 存在一个减半压缩区间
存在一个减半压缩区间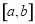 ,(
,(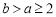 ),则实数m的取值范围是( )
),则实数m的取值范围是( )
A.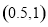 B.
B.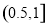 C.
C.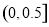 D.
D.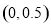
查看答案和解析>>
科目:高中数学 来源:2014-2015学年宁夏银川市高一上学期9月月考数学试卷(解析版) 题型:解答题
(本小题满分10分)已知集合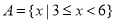 ,
,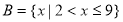 .
.
(Ⅰ)求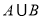 ,
,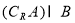 ;
;
(Ⅱ)已知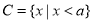 ,若
,若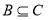 ,求实数
,求实数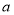 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com