
 ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为 .每人各投4个球,两人投篮命中的概率互不影响.
.每人各投4个球,两人投篮命中的概率互不影响. 分,求乙所得分数
分,求乙所得分数 的概率分布和数学期望.
的概率分布和数学期望. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
| 日最高气温t (单位:℃) | t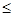 22℃ 22℃ | 22℃<t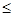 28℃ 28℃ | 28℃<t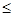 32℃ 32℃ | 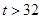 ℃ ℃ |
| 天数 | 6 | 12 | 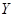 | 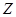 |
| 日最高气温t (单位:℃) | t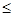 22℃ 22℃ | 22℃<t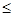 28℃ 28℃ | 28℃<t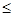 32℃ 32℃ | 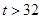 ℃ ℃ |
日销售额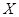 (千元) (千元) | 2 | 5 | 6 | 8 |
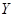 ,
, 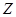 的值;
的值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 答对题目个数 | 0 | 1 | 2 | 3 |
| 人数 | 5 | 10 | 20 | 15 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
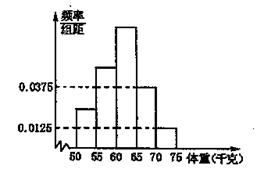
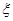 表示体重超过60千克的学生人数,求
表示体重超过60千克的学生人数,求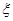 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 请假次数 |  |  |  |  |
| 人数 |  |  |  |  |
 表示这两人请假次数之和,记“函数
表示这两人请假次数之和,记“函数 在区间
在区间 上有且只有一个零点”为事件
上有且只有一个零点”为事件 ,求事件
,求事件 发生的概率
发生的概率 ;
; 表示这两人请假次数之差的绝对值,求随机变量
表示这两人请假次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的”闯关”游戏.
的”闯关”游戏. 
 则闯关成功.
则闯关成功. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 选
选 考核(即共
考核(即共 项测试,随机选取
项测试,随机选取 项),若全部合格,则颁发合格证;若不合格,则重新参加下期的
项),若全部合格,则颁发合格证;若不合格,则重新参加下期的 选
选 考核,直至合格为止,若学生小李抽到“引体向上”一项,则第一次参加考试合格的概率为
考核,直至合格为止,若学生小李抽到“引体向上”一项,则第一次参加考试合格的概率为 ,第二次参加考试合格的概率为
,第二次参加考试合格的概率为 ,第三次参加考试合格的概率为
,第三次参加考试合格的概率为 ,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.
,若第四次抽到可要求调换项目,其它选项小李均可一次性通过. ;
; 分布列.
分布列.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com