
分析 (1)设半焦距为c(c>0),利用离心率,短半轴,求出a,b,顶点椭圆C1的标准方程,设抛物线C2的标准方程为y2=2px(p>0),求出p,顶点抛物线C2的标准方程.
(2)由题意易得两条直线的斜率存在且不为0,设其中一条直线l1的斜率为k,直线l1方程为y=k(x-1),则另一条直线l2的方程为$y=-\frac{1}{k}(x-1)$,联立$\left\{\begin{array}{l}y=k(x-1)\\{y^2}=8x\end{array}\right.$得k2x2-(2k2+8)x+k2=0,△=32k2+64>0,设直线l1与抛物线C2的交点为A,B,则$|AB|=\frac{{4\sqrt{{k^2}+1}•\sqrt{2{k^2}+4}}}{k^2}$,同理求出|CD|=4$\sqrt{{k}^{2}+1}•\sqrt{4{k}^{2}+2}$求出
四边形的面积利用基本不等式求解最值.
解答 解:(1)设半焦距为c(c>0),由题意得$e=\frac{c}{a}=\frac{1}{2},b=2\sqrt{3}$,∴$a=4,b=2\sqrt{3},c=2$,∴椭圆C1的标准方程为$\frac{x^2}{16}+\frac{y^2}{12}=1$.
设抛物线C2的标准方程为y2=2px(p>0),则$\frac{p}{2}=c=2$,∴p=4,∴抛物线C2的标准方程为y2=8x.
(2)由题意易得两条直线的斜率存在且不为0,设其中一条直线l1的斜率为k,直线l1方程为y=k(x-1),则另一条直线l2的方程为$y=-\frac{1}{k}(x-1)$,联立$\left\{\begin{array}{l}y=k(x-1)\\{y^2}=8x\end{array}\right.$得k2x2-(2k2+8)x+k2=0,△=32k2+64>0,设直线l1与抛物线C2的交点为A,B,则$|AB|=\frac{{4\sqrt{{k^2}+1}•\sqrt{2{k^2}+4}}}{k^2}$,同理设直线l2与抛物线C2的交点为C,D,则,|CD|=$\frac{4\sqrt{(-\frac{1}{k})^{2}+1}•\sqrt{2(-\frac{1}{k})^{2}+4}}{(-\frac{1}{k})^{2}}$=4$\sqrt{{k}^{2}+1}•\sqrt{4{k}^{2}+2}$
∴四边形的面积$S=\frac{1}{2}|AB|•|CD|=\frac{1}{2}×\frac{{4\sqrt{{k^2}+1}•\sqrt{2{k^2}+4}}}{k^2}×4\sqrt{{k^2}+1}•\sqrt{4{k^2}+2}$=$\frac{{8({k^2}+1)\sqrt{8{k^4}+20{k^2}+8}}}{k^2}$=$16\sqrt{\frac{{({k^4}+2{k^2}+1)(2{k^4}+5{k^2}+2)}}{k^4}}=16\sqrt{({k^2}+2+\frac{1}{k^2})(2{k^2}+5+\frac{2}{k^2})}$,令$t={k^2}+2+\frac{1}{k^2}$,则t≥4(当且仅当k=±1时等号成立),$S=16\sqrt{t(2t+1)}≥16\sqrt{4•9}=96$.
∴当两直线的斜率分别为1和-1时,四边形的面积最小,最小值为96.
点评 本题考查题意方程的求法抛物线的求法,直线与题意以及抛物线的位置关系的综合应用,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 02 | B. | 13 | C. | 42 | D. | 44 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1] | B. | (-∞,1] | C. | [1,3) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
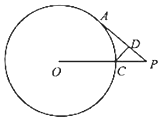 如图,过圆O外一点P作圆O的切线PA,切点为A,连接OP与圆O交于点C,过点C作圆O作AP的垂线,垂足为D,若PA=2$\sqrt{5}$,PC:PO=1:3,求CD的长.
如图,过圆O外一点P作圆O的切线PA,切点为A,连接OP与圆O交于点C,过点C作圆O作AP的垂线,垂足为D,若PA=2$\sqrt{5}$,PC:PO=1:3,求CD的长.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
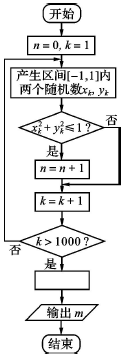
| A. | $m=1-\frac{n}{1000}$ | B. | $m=\frac{n}{1000}$ | C. | $m=1-\frac{n}{250}$ | D. | $m=\frac{n}{250}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com