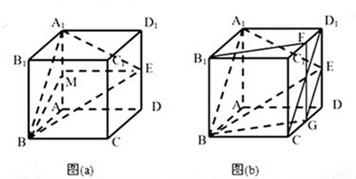
分析:(I)先取AA1的中点M,连接EM,BM,根据中位线定理可知EM∥AD,而AD⊥平面ABB1A1,则EM⊥面ABB1A1,从而BM为直线BE在平面ABB1A1上的射影,则∠EBM直线BE与平面ABB1A1所成的角,设正方体的棱长为2,则EM=AD=2,BE=3,于是在Rt△BEM中,求出此角的正弦值即可.
(II)在棱C1D1上存在点F,使B1F平面A1BE,分别取C1D1和CD的中点F,G,连接EG,BG,CD1,FG,因A1D1∥B1C1∥BC,且A1D1=BC,所以四边形A1BCD1为平行四边形,根据中位线定理可知EG∥A1B,从而说明A1,B,G,E共面,则BG?面A1BE,根据FG∥C1C∥B1G,且FG=C1C=B1B,从而得到四边形B1BGF为平行四边形,则B1F∥BG,而B1F?平面A1BE,BG?平面A1BE,根据线面平行的判定定理可知B1F∥平面A1BE.
解答:解:(I)如图(a),取AA
1的中点M,连接EM,BM,因为E是DD
1的中点,四边形ADD
1A
1为正方形,所以EM∥AD.
又在正方体ABCD-A
1B
1C
1D
1中.AD⊥平面ABB
1A
1,所以EM⊥面ABB
1A
1,从而BM为直线BE在平面ABB
1A
1上的射影,
∠EBM直线BE与平面ABB
1A
1所成的角.
设正方体的棱长为2,则EM=AD=2,BE=
=3,
于是在Rt△BEM中,
sin∠EBM==即直线BE与平面ABB
1A
1所成的角的正弦值为
.
(II)在棱C
1D
1上存在点F,使B
1F平面A
1BE,
事实上,如图(b)所示,分别取C
1D
1和CD的中点F,G,连接EG,BG,CD
1,FG,
因A
1D
1∥B
1C
1∥BC,且A
1D
1=BC,所以四边形A
1BCD
1为平行四边形,
因此D
1C∥A
1B,又E,G分别为D
1D,CD的中点,所以EG∥D
1C,从而EG∥A
1B,这说明A
1,B,G,E共面,所以BG?A
1BE
因四边形C
1CDD
1与B
1BCC
1皆为正方形,F,G分别为C
1D
1和CD的中点,所以FG∥C
1C∥B
1G,且FG=C
1C=B
1B,因此四边形B
1BGF为平行四边形,所以B
1F∥BG,而B
1F?平面A
1BE,BG?平面A
1BE,故B
1F∥平面A
1BE.
点评:本题考查直线与平面所成的角,直线与平面平行,考查考生探究能力、空间想象能力.

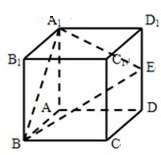 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.


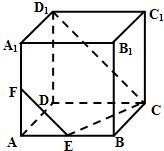 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点 (2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )
(2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )