
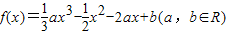
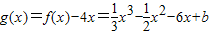 ,然后利用导数求出函数的两个极值点,要使f(x)图象与y=4x有三个公共点,只需极大值大于0,极小值小于0,建立关系式,即可求出b的范围.
,然后利用导数求出函数的两个极值点,要使f(x)图象与y=4x有三个公共点,只需极大值大于0,极小值小于0,建立关系式,即可求出b的范围.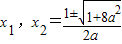
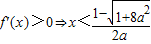 或
或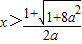
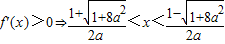
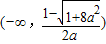 ,
,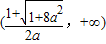 上递增
上递增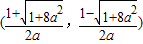 上递增
上递增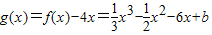
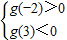
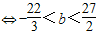 ,即b的取值范围为
,即b的取值范围为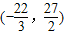


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
| 2m-1-mx | x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2m-1-mx | x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| x |
| 1 |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:中学教材全解 高中数学 必修1(人教A版) 人教A版 题型:044
已知函数![]() .
.
(1)求图象的开口方向,对称轴,顶点坐标,与x轴交点坐标.
(2)求函数的单调区间,最值,零点.
(3)设图象与x轴相交于点(x1,0),(x2,0),不求出根,求|x1-x2|.
(4)已知![]() ,不计算函数值,求
,不计算函数值,求![]() .
.
(5)不计算函数值,试比较![]() 与
与![]() 的大小.
的大小.
(6)写出使函数值为负数的自变量x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() ,
,
(1)若函数![]() 在[l,+∞]上是增函数,求实数
在[l,+∞]上是增函数,求实数![]() 的取值范围。
的取值范围。
(2)若![]() =一
=一![]() 是
是![]() 的极值点,求
的极值点,求![]() 在[l,
在[l,![]() ]上的最大值:
]上的最大值:
(3)在(2)的条件下,是否存在实数b,使得函数g(![]() )=b
)=b![]() 的图像与函
的图像与函![]() 的图像恰有3个交点,若存在,求出实数b的取值范围:若不存在,试说明理由。
的图像恰有3个交点,若存在,求出实数b的取值范围:若不存在,试说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com