
【题目】已知![]() 是自然对数的底数,
是自然对数的底数, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)设![]() ,求
,求![]() 的极值;
的极值;
(2)设![]() ,求证:函数
,求证:函数![]() 没有零点;
没有零点;
(3)若![]() ,设
,设![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】试题分析:(1)![]() ,求其导数并求导数为0的
,求其导数并求导数为0的![]() 值,判断两侧的单调性求极值;(2)
值,判断两侧的单调性求极值;(2)![]() ,
, ![]() ,因为
,因为![]() ,所以
,所以![]() 是减函数,根据导数求函数的单调区间和函数的最大值,判断其最大值小于0;(3)函数
是减函数,根据导数求函数的单调区间和函数的最大值,判断其最大值小于0;(3)函数![]() ,要证明
,要证明![]() ,设函数
,设函数![]() ,根据导数判断函数的单调性以及函数的最小值,证明最小值大于0.
,根据导数判断函数的单调性以及函数的最小值,证明最小值大于0.
试题解析:(1)∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() .
.
∴![]() ,由
,由![]() 得
得![]() .
.
∵![]() 是自然对数的底数,∴
是自然对数的底数,∴![]() 是增函数.
是增函数.
∴当![]() 时,
时, ![]() ,即
,即![]() 是减函数;
是减函数;
当![]() 时,
时, ![]() ,即
,即![]() 是增函数.
是增函数.
∴函数![]() 没有极大值,只有极小值,且当
没有极大值,只有极小值,且当![]() 时,
时, ![]() 取得极小值.
取得极小值.
∴![]() 的极小值为
的极小值为![]() .
.
(2)∵![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 是减函数.
是减函数.
由![]() 解得
解得![]() .
.
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 是增函数,
是增函数,
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 是减函数,
是减函数,
∴当![]() 时,函数
时,函数![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴当![]() 时,函数
时,函数![]() 没有零点.
没有零点.
(3)∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
设![]() ,则
,则![]() .
.
设![]() ,则
,则![]() .
.
∵![]() ,∴
,∴![]() .
.
又∵当![]() 时,
时, ![]() ,∴函数
,∴函数![]() 在
在![]() 上是增函数.
上是增函数.
∵![]() ,∴
,∴![]() ,即
,即![]() .
.
又∵![]() ,
, ![]() ,
,
∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
∴函数![]() 在
在![]() 上是增函数.
上是增函数.
∴当![]() 时,
时, ![]() ,即
,即![]() .
.
∴当![]() 时,
时, ![]() .
.


科目:高中数学 来源: 题型:
【题目】已知空间三点A(0,2,3),B(﹣2,1,6),C(1,﹣1,5);求:
(1)求以向量 ![]() 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;
(2)若向量a分别与向量 ![]() 垂直,且|a|=
垂直,且|a|= ![]() ,求向量a的坐标.
,求向量a的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为对数函数,并且它的图象经过点(2 ![]() ,
, ![]() ),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
(1)求函数f(x)的解析式;
(2)求函数y=g(x)在区间[ ![]() ,16]上的最小值.
,16]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(4x+1)﹣x,g(x)=log2a+log2(2x﹣ ![]() )(a>0,x>1).
)(a>0,x>1).
(1)证明函数f(x)为偶函数;
(2)若函数f(x)﹣g(x)只有一个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在![]() 的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
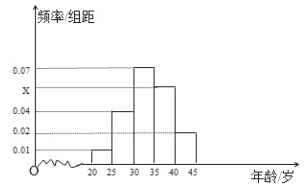
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=  ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,函数g(x)=b﹣f(2﹣x),其中b∈R,若函数y=f(x)﹣g(x)恰有4个零点,则b的取值范围是( )
,函数g(x)=b﹣f(2﹣x),其中b∈R,若函数y=f(x)﹣g(x)恰有4个零点,则b的取值范围是( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞, ![]() )
)
C.(0, ![]() )
)
D.( ![]() ,2)
,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】六个面都是平行四边形的四棱柱称为平行六面体.已知在平行四边形ABCD中(如图1),有AC2+BD2=2(AB2+AD2),则在平行六面体ABCD﹣A1B1C1D1中(如图2),AC12+BD12+CA12+DB12等于( ) 
A.2(AB2+AD2+AA12)
B.3(AB2+AD2+AA12)
C.4(AB2+AD2+AA12)
D.4(AB2+AD2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com