
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,函数
时,函数![]() 有零点,求实数
有零点,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)0.
;(2)0.
【解析】试题分析:(1)![]() 在
在![]() 上为增函数,等价于
上为增函数,等价于![]() 在
在![]() 上恒成立,分类讨论,当
上恒成立,分类讨论,当![]() 时,由函数
时,由函数![]() 的定义域可知,必须有
的定义域可知,必须有![]() 对
对![]() 恒成立,故只能
恒成立,故只能![]() ,所以
,所以![]() 在
在![]() 上恒成立,构造函数
上恒成立,构造函数![]() ,要使
,要使![]() 在
在![]() 上恒成立,只要
上恒成立,只要![]() 即可,从而可求实数
即可,从而可求实数![]() 的取值范围;(2)当
的取值范围;(2)当![]() 时,方程
时,方程![]() 有实根,等价于
有实根,等价于![]() 在
在![]() 上有解,即求
上有解,即求![]() 的值域.构造
的值域.构造![]() (
(![]() ),证明
),证明![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,即可得出结论.
上为减函数,即可得出结论.
试题解析:(1)∵函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
∴![]() 在区间
在区间![]() 上恒成立,
上恒成立,
①当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上为增函数,故
上为增函数,故![]() 符合题意.
符合题意.
②当![]() 时,由函数
时,由函数![]() 的定义域可知
的定义域可知![]() 对
对![]() 恒成立,
恒成立,
故只能![]() ,∴
,∴![]() 在
在![]() 上恒成立,
上恒成立,
令函数![]() ,其对称轴为
,其对称轴为![]() ,
,
∵![]() ,∴
,∴![]() ,要使
,要使![]() 在
在![]() 上恒成立,只要
上恒成立,只要![]() 即可,
即可,
即![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,综上所述,
,综上所述,![]() 的取值范围为
的取值范围为![]() .
.
(2)当![]() 时,函数
时,函数![]() 有零点等价于方程:
有零点等价于方程:
![]() 有实根,
有实根,![]() 可化为:
可化为:
![]() .
.
等价于![]() 在
在![]() 上有解,
上有解,
即求函数![]() 的值域,
的值域,
∵函数![]() ,
,
令函数![]() ,则
,则![]() ,
,
∴当![]() 时,
时,![]() ,从而函数
,从而函数![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]() ,从而函数
,从而函数![]() 在
在![]() 上为减函数,
上为减函数,
因此![]() ,而
,而![]() ,∴
,∴![]() ,
,
故当![]() 时,
时,![]() 取得最大值0.
取得最大值0.


科目:高中数学 来源: 题型:
【题目】线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
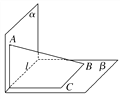
A. 30° B. 45°
C. 60° D. 75°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经营一批进价为![]() 元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
销售价( |
|
|
|
|
日销售量( |
|
|
|
|
日销售额( |
| |||
日销售利润( |
|
(1)在下面给出的直角坐标系中,根据表中的数据描出实数对![]() 的对应点,并写出
的对应点,并写出![]() 与
与![]() 的一个函数关系式;
的一个函数关系式;
(2)请把表中的空格里的数据填上;
(3)根据表中的数据求![]() 与
与![]() 的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称为“局部奇函数”
,则称为“局部奇函数”
(1)已知二次函数![]() (
(![]() 且
且![]() ),试判断
),试判断![]() 是否为“局部奇函数”,并说明理由;
是否为“局部奇函数”,并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域为
为定义域为![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A是实数集,满足若a∈A,则![]() ∈A,a≠1,且1A.
∈A,a≠1,且1A.
(1)若2∈A,则集合A中至少还有几个元素?求出这几个元素.
(2)集合A中能否只含有一个元素?请说明理由.
(3)若a∈A,证明:1-![]() ∈A.
∈A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义满足“如果a∈A,b∈A,那么a±b∈A,且ab∈A,且![]() ∈A(b≠0)”的集合A为“闭集”.试问数集N,Z,Q,R是否分别为“闭集”?若是,请说明理由;若不是,请举反例说明.
∈A(b≠0)”的集合A为“闭集”.试问数集N,Z,Q,R是否分别为“闭集”?若是,请说明理由;若不是,请举反例说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是长方形,侧棱
是长方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,过D作
,过D作![]() 于F,过F作
于F,过F作![]() 交 PC于E.
交 PC于E.
(Ⅰ)证明:![]() 平面PBC;
平面PBC;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
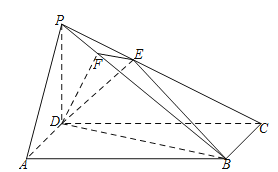
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com