
【题目】某蛋糕店计划按天生产一种面包,每天生产量相同,生产成本每个6元,售价每个8元,未售出的面包降价处理,以每个5元的价格当天全部处理完.
(1)若该蛋糕店一天生产30个这种面包,求当天的利润y(单位:元)关于当天需求量n(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)蛋糕店记录了30天这种面包的日需求量(单位:个),整理得表:
日需求量n | 28 | 29 | 30 | 31 | 32 | 33 |
频数 | 3 | 4 | 6 | 6 | 7 | 4 |
假设蛋糕店在这30天内每天生产30个这种面包,求这30天的日利润(单位:元)的平均数及方差;
(3)蛋糕店规定:若连续10天的日需求量都不超过10个,则立即停止这种面包的生产,现给出连续10天日需求量的统计数据为“平均数为6,方差为2”,试根据该统计数据决策是否一定要停止这种面包的生产?并给出理由.
【答案】(1)![]() ,
,![]() ;(2)平均数为
;(2)平均数为![]() (元),方差为
(元),方差为![]() ;(3)一定要停止,理由见解析
;(3)一定要停止,理由见解析
【解析】
(1)当天需求量![]() 时,当天的利润
时,当天的利润![]() ,当天需求量
,当天需求量![]() 时,当天的利润
时,当天的利润![]() ,由此能求出当天的利润y关于当天需求量n的函数解析式.
,由此能求出当天的利润y关于当天需求量n的函数解析式.
(2)由题意,利用平均数和方差的公式,即可求出这30天的日利润的平均数和方差.
(3)根据该统计数据,一定要停止这种面包的生产.推导出连续10天的日需求量都不超过10个,由此说明一定要停止这种面包的生产.
(1)由题意可知,当天需求量![]() 时,当天的利润
时,当天的利润![]() ,
,
当天需求量![]() 时,当天的利润
时,当天的利润![]() .
.
故当天的利润y关于当天需求量n的函数解析式为:![]() ,
,![]() .
.
(2)由题意可得:
日需求量n | 28 | 29 | 30 | 31 | 32 | 33 |
日利润 | 54 | 57 | 60 | 60 | 60 | 60 |
频数 | 3 | 4 | 6 | 6 | 7 | 4 |
所以这30天的日利润的平均数为![]() (元),
(元),
方差为![]() .
.
(3)根据该统计数据,一定要停止这种面包的生产.理由如下:
由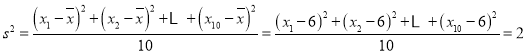 ,
,
可得![]() ,
,
所以![]() (
(![]() ,
,![]() ,
,![]() ),所以
),所以![]() ,
,
由此可以说明连续10天的日需求量都不超过10个,即说明一定要停止这种面包的生产.


科目:高中数学 来源: 题型:
【题目】随着时代的发展和社会的进步,“农村淘宝”发展十分迅速,促进“农产品进城”和“消费品下乡”.“农产品进城”很好地解决了农产品与市场的对接问题,使农民收入逐步提高,生活水平得到改善,农村从事网店经营的人收入逐步提高.西凤脐橙是四川省南充市的特产,因果实呈椭圆形、色泽橙红、果面光滑、无核、果肉脆嫩化渣、汁多味浓,深受人们的喜爱.为此小王开网店销售西凤脐橙,每月月初购进西凤脐橙,每售出1吨西凤脐橙获利润800元,未售出的西凤脐橙,每1吨亏损500元.经市场调研,根据以往的销售统计,得到一个月内西凤脐橙市场的需求量的频率分布直方图如图所示.小王为下一个月购进了100吨西凤脐橙,以x(单位:吨)表示下一个月内市场的需求量,y(单位:元)表示下一个月内经销西凤脐橙的销售利润.
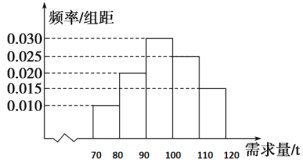
(1)将y表示为x的函数;
(2)根据频率分布直方图估计小王的网店下一个月销售利润y不少于67000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率,(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求小王的网店下一个月销售利润y的分布列和数学期望.
的频率),求小王的网店下一个月销售利润y的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 为椭圆上一动点(异于左右顶点),
为椭圆上一动点(异于左右顶点),![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 两点,问
两点,问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数![]() (其中
(其中![]() )的图象如图所示,为了得到
)的图象如图所示,为了得到![]() 的图象,则只要将
的图象,则只要将![]() 的图象上所有的点( )
的图象上所有的点( )

A.向左平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
B.向左平移![]() 个单位长度,纵坐标伸长到原来的3倍横坐标不变
个单位长度,纵坐标伸长到原来的3倍横坐标不变
C.向右平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
D.向右平移![]() 个单位长度,纵坐标伸长到原来的3倍,横坐标不变
个单位长度,纵坐标伸长到原来的3倍,横坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
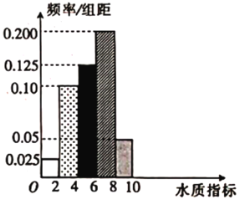
【题目】新《水污染防治法》已由中华人民共和国第十二届全国人民代表大会常务委员会第二十八次会议于2017年6月27日通过,自2018年1月1日起施行.2018年3月1日,某县某质检部门随机抽取了县域内100眼水井,检测其水质总体指标.
罗斯水质指数 | 02 | 24 | 46 | 68 | 810 |
水质状况 | 腐败污水 | 严重污染 | 污染 | 轻度污染 | 纯净 |
(1)求所抽取的100眼水井水质总体指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
(2)①由直方图可以认为,100眼水井水质总体指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在(5.21,5.99)内的概率;
落在(5.21,5.99)内的概率;
②将频率视为概率,若某乡镇抽查5眼水井的水质,记这5眼水井水质总体指标值位于(6,10)内的井数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100眼水井总体指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点(如图1).将
的中点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 的中点(如图2).
的中点(如图2).
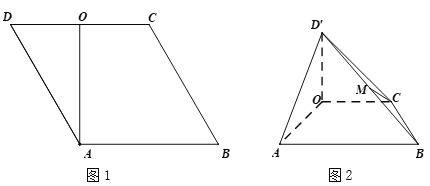
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)当四棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定每年的![]() 月
月![]() 日以后的
日以后的![]() 天为当年的暑假.某钢琴培训机构对
天为当年的暑假.某钢琴培训机构对![]() 位钢琴老师暑假一天的授课量进行了统计,如下表所示:
位钢琴老师暑假一天的授课量进行了统计,如下表所示:
授课量(单位:小时) |
|
|
|
|
|
频数 |
|
|
|
|
|
培训机构专业人员统计近![]() 年该校每年暑假
年该校每年暑假![]() 天的课时量情况如下表:
天的课时量情况如下表:
课时量(单位:天) |
|
|
|
|
|
频数 |
|
|
|
|
|
(同组数据以这组数据的中间值作代表)
(1)估计![]() 位钢琴老师一日的授课量的平均数;
位钢琴老师一日的授课量的平均数;
(2)若以(1)中确定的平均数作为上述一天的授课量.已知当地授课价为![]() 元/小时,每天的各类生活成本为
元/小时,每天的各类生活成本为![]() 元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师
元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师![]() 天暑假授课利润不少于
天暑假授课利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com