
ĄžĖâÄŋĄŋĐÂĄļËŽÎÛČžˇĀÖΡ¨ĄˇŌŅĶÉÖĐģĒČËÃņš˛ēÍšúĩÚĘŽļūŊėČĢšúČËÃņ´úąí´ķģáŗŖÎņÎ¯ÔąģáĩÚļūĘŽ°Ë´ÎģáŌéĶÚ2017Äę6ÔÂ27ČÕͨšũŖŦ×Ô2018Äę1ÔÂ1ČÕÆđĘŠĐĐŖŽ2018Äę3ÔÂ1ČÕŖŦÄŗĪØÄŗÖĘŧė˛ŋÃÅËæģúŗéČĄÁËĪØĶōÄÚ100ŅÛËŽžŽŖŦŧė˛âÆäËŽÖĘ×ÜĖåÖ¸ąęŖŽ
ÂŪ˚ˎÖĘÖ¸Ęũ | 02 | 24 | 46 | 68 | 810 |
ËŽÖĘ×´ŋö | ¸¯°ÜÎÛËŽ | ŅĪÖØÎÛČž | ÎÛČž | ĮáļČÎÛČž | ´ŋžģ |
Ŗ¨1ŖŠĮķËųŗéČĄĩÄ100ŅÛËŽžŽËŽÖĘ×ÜĖåÖ¸ąęÖĩĩÄŅųąžÆŊžųĘũ![]() Ŗ¨ÍŦŌģ×éÖĐĩÄĘũžŨĶøÃ×éĮøŧäĩÄÖĐĩãÖĩ×÷´úąíŖŠŖŽ
Ŗ¨ÍŦŌģ×éÖĐĩÄĘũžŨĶøÃ×éĮøŧäĩÄÖĐĩãÖĩ×÷´úąíŖŠŖŽ
Ŗ¨2ŖŠĸŲĶÉÖąˇŊÍŧŋÉŌÔČĪÎĒŖŦ100ŅÛËŽžŽËŽÖĘ×ÜĖåÖ¸ąęÖĩ![]() ˇū´ĶÕũĖŦˇÖ˛ŧ
ˇū´ĶÕũĖŦˇÖ˛ŧ![]() ŖŦĀûĶøÃÕũĖŦˇÖ˛ŧŖŦĮķ
ŖŦĀûĶøÃÕũĖŦˇÖ˛ŧŖŦĮķ![]() ÂäÔÚŖ¨5.21ŖŦ5.99ŖŠÄÚĩĸÅÂĘŖģ
ÂäÔÚŖ¨5.21ŖŦ5.99ŖŠÄÚĩĸÅÂĘŖģ
ĸÚŊĢÆĩÂĘĘĶÎĒ¸ÅÂĘŖŦČôÄŗĪįÕōŗé˛é5ŅÛËŽžŽĩÄËŽÖĘŖŦŧĮÕâ5ŅÛËŽžŽËŽÖĘ×ÜĖåÖ¸ąęÖĩÎģĶÚŖ¨6ŖŦ10ŖŠÄÚĩÄžŽĘũÎĒ![]() ŖŦĮķ
ŖŦĮķ![]() ĩġֲŧÁĐēÍĘũŅ§ÆÚÍûŖŽ
ĩġֲŧÁĐēÍĘũŅ§ÆÚÍûŖŽ
¸ŊŖēĸŲŧÆËãĩÃËųŗé˛éĩÄÕâ100ŅÛËŽžŽ×ÜĖåÖ¸ąęĩÄąę×ŧ˛îÎĒ![]() Ŗģ
Ŗģ
ĸÚČô![]() ŖŦÔō
ŖŦÔō![]() ŖŦ
ŖŦ![]() ŖŽ
ŖŽ
Ąž´đ°¸ĄŋŖ¨1ŖŠ5.6ŖģŖ¨2ŖŠĸŲ![]() ŖģĸÚˇÖ˛ŧÁĐŧûŊâÎöŖŦ
ŖģĸÚˇÖ˛ŧÁĐŧûŊâÎöŖŦ![]() ŖŽ
ŖŽ
ĄžŊâÎöĄŋ
Ŗ¨1ŖŠ¸ųžŨÆĩÂʡֲŧÖąˇŊÍŧÖĐÆŊžųĘũĩÄĮķŊâˇŊˇ¨ŖŦŧ´ŋÉČŨŌ×ĮķĩÃŊášûŖģ
Ŗ¨2ŖŠĸŲ¸ųžŨĖâŌâŖŦĶÉÕũĖŦˇÖ˛ŧĩĸÅÂĘĮķŊâšĢĘŊŖŦŧ´ŋÉĮķĩÃŊášûŖģ
ĸÚČŨŌ×ÖĒ![]() ˇū´ĶļūĪîˇÖ˛ŧŖŦĪČĮķĩÃ
ˇū´ĶļūĪîˇÖ˛ŧŖŦĪČĮķĩÃ![]() ĩÄČĄÖĩŖŦĮķĩÃļÔĶĻČĄÖĩĩĸÅÂĘŖŦģņĩÃˇÖ˛ŧÁĐŖŦÔŲĮķĘũŅ§ÆÚÍûŧ´ŋÉ.
ĩÄČĄÖĩŖŦĮķĩÃļÔĶĻČĄÖĩĩĸÅÂĘŖŦģņĩÃˇÖ˛ŧÁĐŖŦÔŲĮķĘũŅ§ÆÚÍûŧ´ŋÉ.
Ŗ¨1ŖŠËųŗéČĄĩÄ100ŅÛËŽžŽ×ÜĖåÖ¸ąęÖĩĩÄŅųąžÆŊžųĘũ
![]() ŖŽ
ŖŽ
Ŗ¨2ŖŠĸŲĄß![]() ˇū´ĶÕũĖŦˇÖ˛ŧ
ˇū´ĶÕũĖŦˇÖ˛ŧ![]() ŖŦĮŌ
ŖŦĮŌ![]() ŖŦ
ŖŦ![]() ŖŦ
ŖŦ
Ąā![]() ŖŦ
ŖŦ
Ąā![]() ÂäÔÚ
ÂäÔÚ![]() ÄÚĩĸÅÂĘÔŧĘĮ
ÄÚĩĸÅÂĘÔŧĘĮ![]() ŖŽ
ŖŽ
ĸÚ¸ųžŨĖâŌâĩÃ![]() ŖŦ
ŖŦ
![]() Ŗģ
Ŗģ![]() Ŗģ
Ŗģ
![]() Ŗģ
Ŗģ![]() Ŗģ
Ŗģ
![]() Ŗģ
Ŗģ![]() ŖŽ
ŖŽ
Ąā![]() ĩġֲŧÁĐÎĒ
ĩġֲŧÁĐÎĒ
| 0 | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
|
Ąā![]() ŖŽ
ŖŽ



| Äęŧļ | ¸ßÖĐŋÎŗĖ | Äęŧļ | ŗõÖĐŋÎŗĖ |
| ¸ßŌģ | ¸ßŌģÃâˇŅŋÎŗĖÍÆŧöŖĄ | ŗõŌģ | ŗõŌģÃâˇŅŋÎŗĖÍÆŧöŖĄ |
| ¸ßļū | ¸ßļūÃâˇŅŋÎŗĖÍÆŧöŖĄ | ŗõļū | ŗõļūÃâˇŅŋÎŗĖÍÆŧöŖĄ |
| ¸ßČũ | ¸ßČũÃâˇŅŋÎŗĖÍÆŧöŖĄ | ŗõČũ | ŗõČũÃâˇŅŋÎŗĖÍÆŧöŖĄ |
ŋÆÄŋŖē¸ßÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋÔÚČņŊĮĄ÷ABCÖĐŖŦaŖŊ2![]() ŖŦ_______ŖŦĮķĄ÷ABCĩÄÖÜŗ¤lĩġļΧŖŽ
ŖŦ_______ŖŦĮķĄ÷ABCĩÄÖÜŗ¤lĩġļΧŖŽ
ÔÚĸŲ![]() (Šcos
(Šcos![]() ŖŦsin
ŖŦsin![]() )ŖŦ
)ŖŦ![]() (cos
(cos![]() ŖŦsin
ŖŦsin![]() )ŖŦĮŌ
)ŖŦĮŌ![]()
![]() ŖŦĸÚcosA(2bŠc)ŖŊacosCŖŦĸÛf(x)ŖŊcosxcos(x
ŖŦĸÚcosA(2bŠc)ŖŊacosCŖŦĸÛf(x)ŖŊcosxcos(x![]() )
)![]() ŖŦf(A)
ŖŦf(A)![]()
×ĸŖēÕâČũ¸öĖõŧūÖĐČÎŅĄŌģ¸öŖŦ˛šŗäÔÚÉĪÃæÎĘĖâÖвĸļÔÆäŊøĐĐĮķŊâŖŽ
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖē¸ßÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋŌŅÖĒē¯Ęũ![]() ŖŽ
ŖŽ
Ŗ¨1ŖŠĖÖÂÛē¯Ęũ![]() ĩÄĩĨĩ÷ĐÔŖģ
ĩÄĩĨĩ÷ĐÔŖģ
Ŗ¨2ŖŠČô![]() ŖŦ
ŖŦ![]() ŖŦĮŌ´æÔÚ˛ģĪāĩČĩÄĘĩĘũ
ŖŦĮŌ´æÔÚ˛ģĪāĩČĩÄĘĩĘũ![]() ŖŦĘšĩÃ
ŖŦĘšĩÃ![]() ŖŦĮķÖ¤
ŖŦĮķÖ¤![]() ĮŌ
ĮŌ![]() ŖŽ
ŖŽ
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖē¸ßÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋļÔĶÚēÜļāČËĀ´ËĩŖŦĖáĮ°ĪûˇŅĩÄČĪĘļĘ×ĪČĘĮÔ´ĶÚĐÅĶÃŋ¨ŖŦÔÚÄĮ¸öš¤×ʲģ¸ßĩÄÄę´úŖŦĐÅĶÃŋ¨žøļÔĘĮÉņÆ÷ŖŦÉÔÎĸ´ķŧūĩÄļĢÎ÷ļŧĘĮŋÉŌÔŅĄÔņĶÃĐÅĶÃŋ¨Ā´ÂōŖŦÉõÖÁĶÚˇÖÆÚÂōŖŦČģēķÂũÂũģšŖĄĪÖÔÚŌøĐĐ´ûŋîŌ˛ĘĮēܡįÃŌĩÄŖŦ´Ķˇŋ´ûĩŊŗĩ´ûĩŊŌģ°ãĩÄĪÖŊđ´ûŖŽĐÅĶÃŋ¨Ą°ēöČįŌģŌš´ēˇįĀ´ĄąŖŦąé˛ŧÁ˸÷´ķĐĄŗĮĘĐĩÄ´ķŊÖĐĄĪīŖŽÎĒÁËŊâĐÅĶÃŋ¨ÔÚ![]() ĘĐĩÄĘšĶÃĮéŋöŖŦÄŗĩ÷˛éģúššŊčÖúÍøÂįŊøĐĐÁËÎĘžíĩ÷˛éŖŦ˛ĸ´Ķ˛ÎĶëĩ÷˛éĩÄÍøĶŅÖĐËæģúŗéČĄÁË100ČËŊøĐĐŗéŅųˇÖÎöŖŦĩÃĩŊČįĪÂ
ĘĐĩÄĘšĶÃĮéŋöŖŦÄŗĩ÷˛éģúššŊčÖúÍøÂįŊøĐĐÁËÎĘžíĩ÷˛éŖŦ˛ĸ´Ķ˛ÎĶëĩ÷˛éĩÄÍøĶŅÖĐËæģúŗéČĄÁË100ČËŊøĐĐŗéŅųˇÖÎöŖŦĩÃĩŊČįĪÂ![]() ÁĐÁĒąíŖ¨ĩĨÎģŖēČËŖŠ
ÁĐÁĒąíŖ¨ĩĨÎģŖēČËŖŠ
žŗŖĘšĶÃĐÅĶÃŋ¨ | Åŧļûģō˛ģĶÃĐÅĶÃŋ¨ | ēĪŧÆ | |
40Ëęŧ°ŌÔĪÂ | 15 | 35 | 50 |
40ËęŌÔÉĪ | 20 | 30 | 50 |
ēĪŧÆ | 35 | 65 | 100 |
Ŗ¨1ŖŠ¸ųžŨŌÔÉĪĘũžŨŖŦÄܡņÔÚˇ¸´íÎķĩĸÅÂʲģŗŦšũ0.10ĩÄĮ°ĖáĪÂČĪÎĒ![]() ĘĐĘšĶÃĐÅĶÃŋ¨ĮéŋöĶëÄęÁäĶĐšØŖŋ
ĘĐĘšĶÃĐÅĶÃŋ¨ĮéŋöĶëÄęÁäĶĐšØŖŋ
Ŗ¨2ŖŠĸŲĪÖ´ĶËųŗéČĄĩÄ40Ëęŧ°ŌÔĪÂĩÄÍøÃņÖĐŖŦ°´Ą°žŗŖĘšĶÃĄąĶ륰Åŧļûģō˛ģĶÃĄąÕâÁŊÖÖĀāĐÍŊøĐСֲãŗéŅųŗéČĄ10ČËŖŦČģēķŖŦÔŲ´ĶÕâ10ČËÖĐËæģúŅĄŗö4ČËÔųËÍģũˇÖŖŦĮķŅĄŗöĩÄ4ČËÖĐÖÁÉŲĶĐ3ČËÅŧļûģō˛ģĶÃĐÅĶÃŋ¨ĩĸÅÂĘŖģ
ĸÚŊĢÆĩÂĘĘĶÎĒ¸ÅÂĘŖŦ´Ķ![]() ĘĐËųĶвÎĶëĩ÷˛éĩÄ40ËęŌÔÉĪĩÄÍøÃņÖĐËæģúŗéČĄ3ČËÔųËÍĀņÆˇŖŦŧĮÆäÖĐžŗŖĘšĶÃĐÅĶÃŋ¨ĩÄČËĘũÎĒ
ĘĐËųĶвÎĶëĩ÷˛éĩÄ40ËęŌÔÉĪĩÄÍøÃņÖĐËæģúŗéČĄ3ČËÔųËÍĀņÆˇŖŦŧĮÆäÖĐžŗŖĘšĶÃĐÅĶÃŋ¨ĩÄČËĘũÎĒ![]() ŖŦĮķËæģúąäÁŋ
ŖŦĮķËæģúąäÁŋ![]() ĩġֲŧÁĐĄĸĘũŅ§ÆÚÍûē͡Ŋ˛îŖŽ
ĩġֲŧÁĐĄĸĘũŅ§ÆÚÍûē͡Ŋ˛îŖŽ
˛ÎŋŧšĢĘŊŖē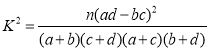 ŖŦÆäÖĐ
ŖŦÆäÖĐ![]() ŖŽ
ŖŽ
˛ÎŋŧĘũžŨŖē
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖē¸ßÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋÄŗĩ°¸âĩęŧÆģŽ°´ĖėÉú˛úŌģÖÖÃæ°üŖŦÃŋĖėÉú˛úÁŋĪāÍŦŖŦÉú˛úŗÉąžÃŋ¸ö6ÔĒŖŦĘÛŧÛÃŋ¸ö8ÔĒŖŦδĘÛŗöĩÄÃæ°üŊĩŧÛ´ĻĀíŖŦŌÔÃŋ¸ö5ÔĒĩÄŧÛ¸ņĩąĖėČĢ˛ŋ´ĻĀíÍę.
Ŗ¨1ŖŠČô¸Ãĩ°¸âĩęŌģĖėÉú˛ú30¸öÕâÖÖÃæ°üŖŦĮķĩąĖėĩÄĀûČķyŖ¨ĩĨÎģŖēÔĒŖŠšØĶÚĩąĖėĐčĮķÁŋnŖ¨ĩĨÎģŖē¸öŖŦ![]() ŖŠĩÄē¯ĘũŊâÎöĘŊŖģ
ŖŠĩÄē¯ĘũŊâÎöĘŊŖģ
Ŗ¨2ŖŠĩ°¸âĩęŧĮÂŧÁË30ĖėÕâÖÖÃæ°üĩÄČÕĐčĮķÁŋŖ¨ĩĨÎģŖē¸öŖŠŖŦÕûĀíĩÃąíŖē
ČÕĐčĮķÁŋn | 28 | 29 | 30 | 31 | 32 | 33 |
ÆĩĘũ | 3 | 4 | 6 | 6 | 7 | 4 |
ŧŲÉčĩ°¸âĩęÔÚÕâ30ĖėÄÚÃŋĖėÉú˛ú30¸öÕâÖÖÃæ°üŖŦĮķÕâ30ĖėĩÄČÕĀûČķŖ¨ĩĨÎģŖēÔĒŖŠĩÄÆŊžųĘũŧ°ˇŊ˛îŖģ
Ŗ¨3ŖŠĩ°¸âĩęšæļ¨ŖēČôÁŦĐø10ĖėĩÄČÕĐčĮķÁŋļŧ˛ģŗŦšũ10¸öŖŦÔōÁĸŧ´ÍŖÖšÕâÖÖÃæ°üĩÄÉú˛úŖŦĪÖ¸øŗöÁŦĐø10ĖėČÕĐčĮķÁŋĩÄÍŗŧÆĘũžŨÎĒĄ°ÆŊžųĘũÎĒ6ŖŦˇŊ˛îÎĒ2ĄąŖŦĘÔ¸ųžŨ¸ÃÍŗŧÆĘũžŨžö˛ßĘĮˇņŌģļ¨ŌĒÍŖÖšÕâÖÖÃæ°üĩÄÉú˛úŖŋ˛ĸ¸øŗöĀíĶÉ.
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖē¸ßÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋÉč![]() ĘĮÁŊ¸öˇĮÁãÆŊÃæĪōÁŋŖŦÔōĶĐŖē
ĘĮÁŊ¸öˇĮÁãÆŊÃæĪōÁŋŖŦÔōĶĐŖē
ĸŲČô![]() ŖŦÔō
ŖŦÔō![]()
ĸÚČô![]() ŖŦÔō
ŖŦÔō![]()
ĸÛČô![]() ŖŦÔō´æÔÚĘĩĘũ
ŖŦÔō´æÔÚĘĩĘũ![]() ŖŦĘšĩÃ
ŖŦĘšĩÃ![]()
ĸÜČô´æÔÚĘĩĘũ![]() ŖŦĘšĩÃ
ŖŦĘšĩÃ![]() ŖŦÔō
ŖŦÔō![]() ģō
ģō![]() ËĸöÃüĖâÖĐÕæÃüĖâĩÄĐōēÅÎĒ __________ŖŽŖ¨ĖîĐ´ËųĶĐÕæÃüĖâĩÄĐōēÅŖŠ
ËĸöÃüĖâÖĐÕæÃüĖâĩÄĐōēÅÎĒ __________ŖŽŖ¨ĖîĐ´ËųĶĐÕæÃüĖâĩÄĐōēÅŖŠ
Ąž´đ°¸ĄŋĸŲĸÛĸÜ
ĄžŊâÎöĄŋÖđŌģŋŧ˛éËų¸øĩÄŊáÂÛŖē
ĸŲČô![]() ŖŦÔō
ŖŦÔō![]() ŖŦžŨ´ËĶĐŖē
ŖŦžŨ´ËĶĐŖē![]() ŖŦËĩˇ¨ĸŲÕũȡŖģ
ŖŦËĩˇ¨ĸŲÕũȡŖģ
ĸÚČô![]() ŖŦČĄ
ŖŦČĄ![]() ŖŦÔō
ŖŦÔō![]() ŖŦ
ŖŦ
ļø![]() ŖŦËĩˇ¨ĸÚ´íÎķŖģ
ŖŦËĩˇ¨ĸÚ´íÎķŖģ
ĸÛČô![]() ŖŦÔō
ŖŦÔō![]() ŖŦžŨ´ËĶĐŖē
ŖŦžŨ´ËĶĐŖē![]() ŖŦ
ŖŦ
ĶÉÆŊÃæĪōÁŋĘũÁŋģũĩÄļ¨ŌåĶĐŖē![]() ŖŦ
ŖŦ
ÔōĪōÁŋ![]() ˇ´ĪōŖŦšĘ´æÔÚĘĩĘũ
ˇ´ĪōŖŦšĘ´æÔÚĘĩĘũ![]() ŖŦĘšĩÃ
ŖŦĘšĩÃ![]() ŖŦËĩˇ¨ĸÛÕũȡŖģ
ŖŦËĩˇ¨ĸÛÕũȡŖģ
ĸÜČô´æÔÚĘĩĘũ![]() ŖŦĘšĩÃ
ŖŦĘšĩÃ![]() ŖŦÔōĪōÁŋ
ŖŦÔōĪōÁŋ![]() ĶëĪōÁŋ
ĶëĪōÁŋ![]() š˛ĪßŖŦ
š˛ĪßŖŦ
´ËĘą![]() ŖŦ
ŖŦ![]() ŖŦ
ŖŦ
ČôĖâÖĐËų¸øĩÄÃüĖâÕũȡŖŦÔō![]() ŖŦ
ŖŦ
¸ÃŊáÂÛÃ÷ĪÔŗÉÁĸ.ŧ´Ëĩˇ¨ĸÜÕũȡŖģ
×ÛÉĪŋÉĩÃŖēÕæÃüĖâĩÄĐōēÅÎĒĸŲĸÛĸÜ.
ĩãžĻŖē´ĻĀíÁŊ¸öĪōÁŋĩÄĘũÁŋģũĶĐČũÖÖˇŊˇ¨ŖēĀûĶÃļ¨ŌåŖģĀûĶÃĪōÁŋĩÄ×øąęÔËËãŖģĀûĶÃĘũÁŋģũĩÄŧ¸ēÎŌâŌåŖŽžßĖåĶĻĶÃĘąŋɸųžŨŌŅÖĒĖõŧūĩÄĖØÕ÷Ā´ŅĄÔņŖŦÍŦĘąŌĒ×ĸŌâĘũÁŋģũÔËËãÂÉĩÄĶĻĶÃŖŽ
ĄžĖâĐÍĄŋĖîŋÕĖâ
ĄžŊáĘøĄŋ
17
ĄžĖâÄŋĄŋŌŅÖĒÔÚ![]() ÖĐŖŦ
ÖĐŖŦ![]() ŖŦĮŌ
ŖŦĮŌ![]() .
.
Ŗ¨1ŖŠĮķŊĮ![]() ĩÄ´ķĐĄŖģ
ĩÄ´ķĐĄŖģ
Ŗ¨2ŖŠÉčĘũÁĐ![]() Âú×ã
Âú×ã![]() ŖŦĮ°
ŖŦĮ°![]() ĪîēÍÎĒ
ĪîēÍÎĒ![]() ŖŦČô
ŖŦČô![]() ŖŦĮķ
ŖŦĮķ![]() ĩÄÖĩ.
ĩÄÖĩ.
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖē¸ßÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋŌĀžŨÄŗĩØÄŗĖõēĶÁ÷8Ô¡ŨĩÄËŽÎÄšÛ˛âĩãĩÄĀúʡÍŗŧÆĘũžŨËųģæÖÆĩÄÆĩÂʡֲŧÖąˇŊÍŧČįÍŧŖ¨ŧ×ŖŠËųĘžŖģŌĀžŨĩąĩØĩÄĩØÖĘššÔėŖŦĩÃĩŊËŽÎģĶëÔÖēĻĩČŧļĩÄÆĩÂʡֲŧĖõĐÎÍŧČįÍŧŖ¨ŌŌŖŠËųĘžŖŽ
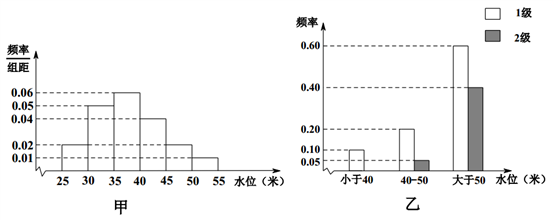
ĘÔšĀŧƸÃēĶÁ÷ÔÚ8Ô¡ŨËŽÎģĩÄÖĐÎģĘũŖģ
Ŗ¨1ŖŠŌÔ´ËÆĩÂĘ×÷ÎĒ¸ÅÂĘŖŦĘÔšĀŧƸÃēĶÁ÷ÔÚ8Ô¡ŨˇĸÉú1ŧļÔÖēĻĩĸÅÂĘŖģ
Ŗ¨2ŖŠ¸ÃēĶÁ÷ĶōÄŗÆķŌĩŖŦÔÚ8Ô¡ŨŖŦČôÃģĘÜ1Ąĸ2ŧļÔÖēĻĶ°ĪėŖŦĀûČķÎĒ500ÍōÔĒŖģČôĘÜ1ŧļÔÖēĻĶ°ĪėŖŦÔōŋ÷Ëđ100ÍōÔĒŖģČôĘÜ2ŧļÔÖēĻĶ°ĪėÔōŋ÷Ëđ1000ÍōÔĒŖŽ
ĪÖ´ËÆķŌĩĶĐČįĪÂČũÖÖĶĻļÔˇŊ°¸Ŗē
ˇŊ°¸ | ˇĀŋØĩČŧļ | ˇŅĶÃŖ¨ĩĨÎģŖēÍōÔĒŖŠ |
ˇŊ°¸Ōģ | ÎŪ´ëĘŠ | 0 |
ˇŊ°¸ļū | ˇĀŋØ1ŧļÔÖēĻ | 40 |
ˇŊ°¸Čũ | ˇĀŋØ2ŧļÔÖēĻ | 100 |
ĘÔÎĘŖŦČįŊö´ĶĀûČķŋŧÂĮŖŦ¸ÃÆķŌĩĶĻŅĄÔņÕâČũÖÖˇŊ°¸ÖĐĩÄÄÄÖÖˇŊ°¸ŖŋËĩÃ÷ĀíĶÉŖŽ
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖē¸ßÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋąąžŠĩØĖú°ËͨĪßÎ÷ÆđËÄģŨÕžŖŦļĢÖÁÍÁĮÅÕžŖŦČĢŗ¤18.964kmŖŦš˛Éč13×ųŗĩÕžŖŽÄŋĮ°°ËͨĪßÖ´ĐĐ2014Äę12ÔÂ28ČÕÖÆļŠĩÄŧÆŧÛąę×ŧŖŦ¸÷ÕžŧäŧÆŗĖÆąŧÛŖ¨ĩĨÎģ:ÔĒŖŠČįĪÂŖē
ËÄģŨ | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
ËÄģŨļĢ | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
¸ßąŽĩę | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | p>5 | |||
´ĢÃŊ´ķŅ§ | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
ËĢĮÅ | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
šÜׯ | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
°ËĀīĮÅ | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
ͨÖŨąąÔˇ | 3 | 3 | 3 | 3 | 3 | ||||||||
šûÔ° | 3 | 3 | 3 | 3 | |||||||||
žÅŋÃĘ÷ | 3 | 3 | 3 | ||||||||||
ĀæÔ° | /p> | 3 | 3 | ||||||||||
ÁŲēĶĀī | 3 | ||||||||||||
ÍÁĮÅ | |||||||||||||
ËÄģŨ | ËÄģŨļĢ | ¸ßąŽĩę | ´ĢÃŊ´ķŅ§ | ËĢĮÅ | šÜׯ | °ËĀīĮÅ | ͨÖŨąąÔˇ | šûÔ° | žÅŋÃĘ÷ | ĀæÔ° | ÁŲēĶĀī | ÍÁĮÅ |
Ŗ¨ĸņŖŠÔÚ13×ųŗĩÕžÖĐČÎŅĄÁŊ¸ö˛ģÍŦĩÄŗĩÕžŖŦĮķÁŊÕžŧäÆąŧÛ˛ģ×ã5ÔĒĩĸÅÂĘŖģ
Ŗ¨ĸōŖŠŧ×ŌŌļūČË´ĶËÄģŨÕžÉĪŗĩŗË×ø°ËͨĪßŖŦ¸÷×ÔČÎŅĄÁíŌģÕžĪÂŗĩŖ¨ļūČËŋÉÍŦÕžĪÂŗĩŖŠŖŦŧĮŧ×ŌŌļūČËŗËŗĩšēÆąģ¨ˇŅÖŽēÍÎĒXÔĒŖŦĮķXĩġֲŧÁĐŖģ
Ŗ¨ĸķŖŠČôŧ×ŌŌļūČËÖģŗË×ø°ËͨĪßŖŦŧ×´ĶËÄģŨÕžÉĪŗĩŖŦČÎŅĄÁíŌģÕžĪÂŗĩŖŦŧĮÆąŧÛÎĒ![]() ÔĒŖģŌŌ´ĶÍÁĮÅÕžÉĪŗĩŖŦČÎŅĄÁíŌģÕžĪÂŗĩŖŦŧĮÆąŧÛÎĒ
ÔĒŖģŌŌ´ĶÍÁĮÅÕžÉĪŗĩŖŦČÎŅĄÁíŌģÕžĪÂŗĩŖŦŧĮÆąŧÛÎĒ![]() ÔĒŖŽĘÔąČŊĪ
ÔĒŖŽĘÔąČŊĪ![]() ēÍ
ēÍ![]() ĩġŊ˛î
ĩġŊ˛î![]() ēÍ
ēÍ![]() ´ķĐĄŖŽŖ¨ŊáÂÛ˛ģĐčŌĒÖ¤Ã÷ŖŠ
´ķĐĄŖŽŖ¨ŊáÂÛ˛ģĐčŌĒÖ¤Ã÷ŖŠ
˛éŋ´´đ°¸ēÍŊâÎö>>
ŋÆÄŋŖē¸ßÖĐĘũŅ§ Ā´Ô´Ŗē ĖâĐÍŖē
ĄžĖâÄŋĄŋÉč![]() Ąĸ
Ąĸ![]() ĘĮŋÕŧäÁŊĖõ˛ģÍŦĩÄÖąĪßŖŦ
ĘĮŋÕŧäÁŊĖõ˛ģÍŦĩÄÖąĪßŖŦ![]() Ąĸ
Ąĸ![]() ĘĮŋÕŧäÁŊ¸ö˛ģÍŦĩÄÆŊÃæŖŽ¸øŗöĪÂÁĐËĸöÃüĖâŖē
ĘĮŋÕŧäÁŊ¸ö˛ģÍŦĩÄÆŊÃæŖŽ¸øŗöĪÂÁĐËĸöÃüĖâŖē
ĸŲČô![]() ŖŦ
ŖŦ![]() ŖŦ
ŖŦ![]() ŖŦÔō
ŖŦÔō![]() Ŗģ
Ŗģ
ĸÚČô![]() ŖŦ
ŖŦ![]() ŖŦ
ŖŦ![]() ŖŦÔō
ŖŦÔō![]() Ŗģ
Ŗģ
ĸÛČô![]() ŖŦ
ŖŦ![]() ŖŦ
ŖŦ![]() ŖŦÔō
ŖŦÔō![]() Ŗģ
Ŗģ
ĸÜČô![]() ŖŦ
ŖŦ![]() ŖŦ
ŖŦ![]() ŖŦ
ŖŦ![]() ŖŦÔō
ŖŦÔō![]() ŖŽ
ŖŽ
ÆäÖĐÕũȡĩÄĘĮ__________Ŗ¨ĖîĐōēÅŖŠŖŽ
˛éŋ´´đ°¸ēÍŊâÎö>>
šúŧĘŅ§ĐŖĶÅŅĄ - ÁˇĪ°˛áÁĐąí - ĘÔĖâÁĐąí
ēūąąĘĄģĨÁĒÍøÎĨˇ¨ēͲģÁŧĐÅĪĸžŲą¨ÆŊĖ¨ | ÍøÉĪĶĐēĻĐÅĪĸžŲą¨×¨Įø | ĩįĐÅÕŠÆžŲą¨×¨Įø | ÉæĀúʡĐéÎŪÖ÷ŌåĶĐēĻĐÅĪĸžŲą¨×¨Įø | ÉæÆķĮÖȨžŲą¨×¨Įø
ÎĨˇ¨ēͲģÁŧĐÅĪĸžŲą¨ĩįģ°Ŗē027-86699610 žŲą¨ĶĘĪäŖē58377363@163.com