
分析 根据条件可得到$\overrightarrow{AD}=-\frac{1}{2}\overrightarrow{BA}$,$\overrightarrow{DF}=\frac{1}{4}(\overrightarrow{BC}-\overrightarrow{BA})$,从而得到$\overrightarrow{AF}=-\frac{3}{4}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}$,代入$\overrightarrow{AF}•\overrightarrow{BC}$进行数量积的运算即可.
解答 解:如图,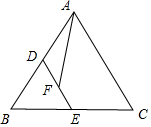
据条件:
$\overrightarrow{AF}=\overrightarrow{AD}+\overrightarrow{DF}$
=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{DE}$
=$-\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{AC}$
=$-\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}(\overrightarrow{BC}-\overrightarrow{BA})$
=$-\frac{3}{4}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}$;
∴$\overrightarrow{AF}•\overrightarrow{BC}=(-\frac{3}{4}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC})•\overrightarrow{BC}$
=$-\frac{3}{4}\overrightarrow{BA}•\overrightarrow{BC}+\frac{1}{4}{\overrightarrow{BC}}^{2}$
=$-\frac{3}{4}×2×2×\frac{1}{2}+\frac{1}{4}×4$
=$-\frac{1}{2}$.
故答案为:$-\frac{1}{2}$.
点评 考查向量加法、减法和数乘的几何意义,向量的数乘和数量积运算,以及数量积的计算公式.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:选择题
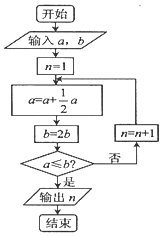 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,8) | C. | (4,8) | D. | [4,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{3}$,$\frac{3}{4}$π) | B. | ($\frac{π}{3}$,$\frac{3}{4}$π] | C. | ($\frac{π}{4}$,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,$\frac{3}{4}$π)∪($\frac{π}{4}$,$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
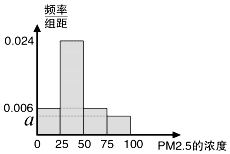 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 3 | 0.15 |
| 第二组 | (25,50] | 12 | 0.6 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com