
分析 (1)求出函数的导数,根据f′(0)=0,求出a的值,检验即可;(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(3)结合(2)得到ln(1+x2)<x,累加即可.
解答 解:(1)∵${f^/}(x)=\frac{2x}{{1+{x^2}}}+a$,
又∵x=0是f(x)的一个极值点,
∴f′(0)=0,∴a=0,验证知a=0符合条件.
(2)∵${f^/}(x)=\frac{2x}{{1+{x^2}}}+a=\frac{{a{x^2}+2x+a}}{{1+{x^2}}}$
①若a=0时,∴f(x)在(0,+∞)单调递增,在(-∞,0)单调递减;
②若$\left\{\begin{array}{l}a<0\\△≤0\end{array}\right.$得,当a≤-1时,f′(x)≤0对x∈R恒成立,
∴f(x)在R上单调递减.
③若-1<a<0时,由f′(x)>0得ax2+2x+a>0
∴$\frac{{-1+\sqrt{1-{a^2}}}}{a}<x<\frac{{-1-\sqrt{1-{a^2}}}}{a}$
再令f′(x)<0,可得$x>\frac{{-1-\sqrt{1-{a^2}}}}{a}或x<\frac{{-1+\sqrt{1-{a^2}}}}{a}$
∴f(x)在$(\frac{{-1+\sqrt{1-{a^2}}}}{a},\frac{{-1-\sqrt{1-{a^2}}}}{a})$上单调递增,
在$(-∞,\frac{{-1+\sqrt{1-{a^2}}}}{a})和(\frac{{-1-\sqrt{1-{a^2}}}}{a},+∞)$上单调递减
综上所述,若a≤-1时,f(x)在(-∞,+∞)上单调递减;
若-1<a<0时,f(x)在$(\frac{{-1+\sqrt{1-{a^2}}}}{a},\frac{{-1-\sqrt{1-{a^2}}}}{a})$上单调递增,
在$(-∞,\frac{{-1+\sqrt{1-{a^2}}}}{a})和(\frac{{-1-\sqrt{1-{a^2}}}}{a},+∞)$上单调递减;
若a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减.
证明:(3)由(2)知,当a=-1时,f(x)在(-∞,+∞)单调递减
当x∈(0,+∞)时,由f(x)<f(0)=0∴ln(1+x2)<x,
∴$ln(1+x)<\sqrt{x}$,
$\begin{array}{l}ln[{(1+\frac{1}{3})(1+\frac{1}{9})…(1+\frac{1}{3^n})}]=ln(1+\frac{1}{3})+ln(1+\frac{1}{9})+…ln(1+\frac{1}{3^n})\\<\sqrt{\frac{1}{3}}+\sqrt{\frac{1}{9}}+…+\sqrt{\frac{1}{3^n}}=\frac{{\frac{1}{{\sqrt{3}}}(1-{{(\frac{1}{{\sqrt{3}}})}^n})}}{{1-\frac{1}{{\sqrt{3}}}}}=\frac{{\sqrt{3}+1}}{2}<\frac{3}{2}\\∴(1+\frac{1}{3})(1+\frac{1}{9})…(1+\frac{1}{3^n})<{e^{\frac{3}{2}}}.\end{array}$
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及不等式的证明,考查转化思想、分类讨论思想,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{4}$ | B. | x=$\frac{π}{2}$ | C. | x=$\frac{π}{6}$ | D. | x=π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | $\sqrt{15}$ | C. | $\sqrt{19}$ | D. | $\sqrt{37}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示:O、A、B是平面上的三点,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,且|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2在平面AOB上,若P为线段AB的中垂线上任意一点,则$\overrightarrow{OP}$•($\overrightarrow{a}$-$\overrightarrow{b}$)的值是( )
如图所示:O、A、B是平面上的三点,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,且|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2在平面AOB上,若P为线段AB的中垂线上任意一点,则$\overrightarrow{OP}$•($\overrightarrow{a}$-$\overrightarrow{b}$)的值是( )| A. | $\frac{5}{2}$ | B. | 5 | C. | 3 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
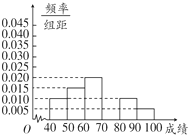 如图是从成都某中学参加高三体育考试的学生中抽出的60名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题:
如图是从成都某中学参加高三体育考试的学生中抽出的60名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com