
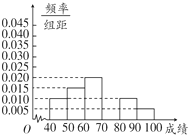
 ��ͼ�Ǵӳɶ�ij��ѧ�μӸ����������Ե�ѧ���г����60��ѧ�������ɼ�����Ϊ��������Ƶ�ʷֲ�ֱ��ͼ����ֱ��ͼǡ��ȱ���˳ɼ�������[70��80���ڵ�ͼ�Σ�����ͼ�ε���Ϣ���ش��������⣺
��ͼ�Ǵӳɶ�ij��ѧ�μӸ����������Ե�ѧ���г����60��ѧ�������ɼ�����Ϊ��������Ƶ�ʷֲ�ֱ��ͼ����ֱ��ͼǡ��ȱ���˳ɼ�������[70��80���ڵ�ͼ�Σ�����ͼ�ε���Ϣ���ش��������⣺���� ��1���ɸ����Ƶ�ʺ͵���1��������ɼ���[70��80���ڵ�Ƶ�ʣ��Ӷ���ȫƵ�ʷֲ�ֱ��ͼ�����ܹ��Ƴ���ѧ���ɼ��ļ����ʣ�
��2��������X�Ŀ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�E��X����
��� �⣺��1����Ϊ�����Ƶ�ʺ͵���1��
�ʳɼ���[70��80���ڵ�Ƶ��Ϊ��
f4=1-��0.01��2+0.015+0.020+0.005����10=0.4��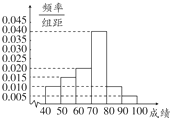 Ƶ�ʷֲ�ֱ��ͼ����ͼ��
Ƶ�ʷֲ�ֱ��ͼ����ͼ��
�����⣬6��0�֣������ϵķ����ڵ������ġ��塢���Σ�
����Ƶ�ʺ�Ϊ��0.02+0.04+0.01+0.005����10=0.75��
�����ѧ���ɼ��ļ�������75%
��2���߳ɼ���[80��90���ڵ�����=0.01��10��60=6��
��ɼ���[80��85����[85��90���ڵ������ֱ�Ϊ4�˺�2�ˣ�
��X�Ŀ���ȡֵΪ0��1��2
P��X=0��=$\frac{{C}_{4}^{3}{C}_{2}^{0}}{{C}_{6}^{3}}$=$\frac{1}{5}$��
P��X=1��=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$��
P��X=2��=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{1}{5}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע��Ƶ�ʷֲ�ֱ��ͼ���ʵĺ������ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{5}$ | B�� | $\frac{4}{5}$ | C�� | $\frac{2}{25}$ | D�� | $\frac{4}{25}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ | B�� | ��Ҫ����� | ||
| C�� | ��Ҫ | D�� | �Ȳ����Ҳ����Ҫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com