
分析 通过求导结合函数的单调性得出不等式组,从而确定m的取值范围.
解答 解:f(x)=x3+($\frac{m}{2}$+2)x2-2x,
∴f′(x)=3x2+(m+4)x-2,
∵f(x)在区间(t,3)上总不是单调函数,且f′(0)=-2,
∴$\left\{\begin{array}{l}{f′(t)<0}\\{f′(3)>0}\end{array}\right.$,
由题意得:对于任意的t∈[1,2],f′(t)<0恒成立,
∴$\left\{\begin{array}{l}{f′(1)<0}\\{f′(2)<0}\\{f′(3)>0}\end{array}\right.$,
∴-$\frac{37}{3}$<m<-9,
故答案为:$(-\frac{37}{3},-9)$.
点评 本题考察了求导函数,讨论函数的单调区间,导函数的应用,是一道中档题.


科目:高中数学 来源: 题型:解答题
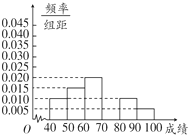 如图是从成都某中学参加高三体育考试的学生中抽出的60名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题:
如图是从成都某中学参加高三体育考试的学生中抽出的60名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x∈Z|x<2} | B. | {x∈Z|0≤x<2} | C. | {1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{3}$) | B. | (-∞,$\frac{1}{3}$] | C. | (0,$\frac{1}{3}$] | D. | (-∞,0)∪(0,$\frac{1}{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com