
我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知 、
、 是一对相关曲线的焦点,
是一对相关曲线的焦点, 是它们在第一象限的交点,当
是它们在第一象限的交点,当 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( )
A. | B.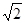 | C. | D.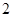 |
A
解析试题分析:记F1P=m,F2P=n,F1F2=2c,由余弦定理得(2c)2=m2+n2-2mncos600,即4c2=m2+n2-mn。
设a1是椭圆的长半轴,a2是双曲线的实半轴,由椭圆及双曲线定义,得m+n=2a1,m-n=2a2,即m=a1+a2,n=a1-a2,将它们及离心率互为倒数关系代入前式得a12-4a1a2+a22=0,可求得a1=3a2,e1×e2=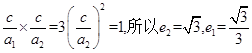 。所以这一对相关曲线中双曲线的离心率是
。所以这一对相关曲线中双曲线的离心率是 。
。
考点:椭圆的简单性质;双曲线的简单性质;余弦定理。
点评:本题考查圆锥曲线的共同特征,考查了椭圆与双曲线的性质,解题的关键是理解定义,且灵活应用定义。本题考查了阅读能力及推理判断的能力,本部分题符号计算多,运算量大,解题时要认真严谨,避免马虎出错。


科目:高中数学 来源: 题型:单选题
设 分别是双曲线
分别是双曲线 的左,右焦点,若在双曲线右支上存在点P,满足
的左,右焦点,若在双曲线右支上存在点P,满足 ,且
,且 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的离心率等于( )
的距离等于双曲线的实轴长,则该双曲线的离心率等于( )
| A.2 | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com