
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 分别求出A、B的坐标,设出P点的坐标,各个关于x的方程,得到解的个数,从而求出满足条件的P点的个数即可.
解答 解:由题意A:(3,0),B(0,3),
设幂函数f(x)的解析式是f(x)=xα,
将(2,4)代入表达式得:α=2,
故f(x)=x2,
设P(x,x2),则P到AB的距离d=$\frac{|x{+x}^{2}-3|}{\sqrt{2}}$,
∴S△ABP=$\frac{1}{2}$•3$\sqrt{2}$•$\frac{|x{+x}^{2}-3|}{\sqrt{2}}$=3,
故x2+x-3=±2,
故x2+x-5=0或x2+x-1=0,
由△=1+20=21>0和△=1+4=5>0,
故可求出四个解,
故P点的坐标有4个,
故选:A.
点评 本题考查了点的直线的距离,考查幂函数的定义以及根的判别式,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | -3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x≠0,则$x+\frac{1}{x}$≥2 | |
| B. | “实数a=1”是“直线x+ay=0与直线x-ay=0互相垂直”的充要条件 | |
| C. | 命题“?x>0,x2-x≤0”的否定是“?x>0,x2-x>0” | |
| D. | 命题“若-1<x<1,则x2<1”的否命题是“若x2≥1,则x≥1或x≤-1” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
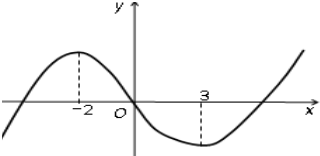
| A. | $({\frac{1}{2},+∞})$ | B. | $({-∞,\frac{1}{2}})$ | C. | (-2,3) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-1)∪(\frac{1}{3},+∞)$ | B. | $(-∞,-2)∪(\frac{2}{3},+∞)$ | C. | $(-2,\frac{2}{3})$ | D. | $(-1,\frac{1}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
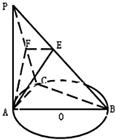 如图,PA垂直⊙O所在的平面,AB为⊙O的直径,C是⊙O上的一点,AE⊥PB与E,AF⊥PC于F,给出下列结论:
如图,PA垂直⊙O所在的平面,AB为⊙O的直径,C是⊙O上的一点,AE⊥PB与E,AF⊥PC于F,给出下列结论:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-7,-3) | B. | [-21,-3] | C. | [-7,-3] | D. | (-21,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com