
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①分别判断命题p,q的真假,结合复合命题真假关系进行判断,
②根据随机变量的期望和方差公式进行求解判断,
③根据充分条件和必要条件的定义进行判断,
④根据正态分布的性质进行求解判断.
解答 解:①若命题p:?x∈R,使得tanx<x,则当x=$\frac{5π}{4}$时,tan$\frac{5π}{4}$=-1,满足tanx<x,故p是真命题,
命题q:?x∈R+,lg2x+lgx+1>0为真命题,
∵判别式△═1-4=-3<0,∴lg2x+lgx+1>0恒成立,则命题“p且?q”是假命题,故①错误,
②若随机变量ξ~B(n,p),由Eξ=6,Dξ=3,得np=6,npq=3,
则q=$\frac{1}{2}$,即p=$\frac{1}{2}$,n=12,
则P(ξ=1)=${C}_{6}^{1}$$•\frac{1}{2}$$•(\frac{1}{2})^{5}$=$\frac{3}{32}$,
则$P(ξ=1)=\frac{3}{4}$错误,故②错误,
③“lgx,lgy,lgz成等差数列”则2lgy=lgx+lgz,即lgy2=lgxy,
则y2=xz,且x,y,z>0,此时y2=xz成立,
反之当x=0,y=0,z=0时,满足y2=xz,但lgx,lgy,lgz无意义,即必要性不成立,
则“lgx,lgy,lgz成等差数列”是“y2=xz”成立的充要条件错误,故③错误,
④已知ξ服从正态分布N(1,22),且P(-1≤ξ<1)=0.3,则P(1≤ξ<3)=P(-1≤ξ<1)=0.3,
则P(ξ≥3)=0.5-P(1≤ξ<3)=0.5-0.3=0.2,故④正确,
故正确的是④,
故选:A
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,难度不大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 650 | B. | 700 | C. | 750 | D. | 800 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
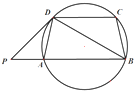 如图,圆内接四边形ABCD满足AB∥CD,P在BA的延长线上,且PD2=PA•PB.若BD=2$\sqrt{2}$,PD=CD=2.
如图,圆内接四边形ABCD满足AB∥CD,P在BA的延长线上,且PD2=PA•PB.若BD=2$\sqrt{2}$,PD=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e-1 | B. | e | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com