
分析 (1)令x=y=1可得f(2)=3;令x=y=0可得f(0)=0或f(0)=-1,令x=1,y=0可得f(1)=f(1)f(0)+f(0)+f(1),若f(0)=-1,则f(1)=f(0)=-1与已知矛盾;
(2)f(2x)-a≥af(x)-5对任意x恒成立⇒f2(x)+2f(x)-a≥af(x)-5对任意x恒成立,先探讨f(x)=t的取值范围t∈(-1,+∞),原不等式等价于:t2+2t-a≥at-5在t∈(-1,+∞)恒成立,(3)
(3)f(f(x))≥$\frac{7-f(x+1)}{1+f(x+1)}$⇒[1+f(x+1)]•f(f(x))≥7-f(x+1)⇒f(x+1)•⇒[1+f(x+1)]•f(f(x))≥7-f(x+1)⇒f(x+1)+f(x+1)•f(f(x))+f(f(x))≥7⇒f(x+1+f(x))≥7.再证明函数 y=f(x)在R上单调递增,原不等式转化为x+1+f(x)≥3令F(x)=x+1+f(x),F(x)在R上单调递增F(x)≥F(3)⇒x≥1,
解答 解:(1)令x=y=1可得f(2)=f(1)f(1)+2f(1)=3,
令x=y=0可得f(0)=f(0)f(0)+2f(0),则f(0)=0或f(0)=-1,
令x=1,y=0可得f(1)=f(1)f(0)+f(0)+f(1),若f(0)=-1,则f(1)=f(0)=-1与已知矛盾,∴f(0)=0;
(2)f(2x)-a≥af(x)-5对任意x恒成立⇒f2(x)+2f(x)-a≥af(x)-5对任意x恒成立,
令f(x)=t,以下探讨f(x)=t的取值范围.
令y=-x可得f(0)=f(-x)f(x)+f(x)+f(-x)⇒f(x)=$\frac{-f(-x)}{f(-x)+1}=-1+\frac{1}{f(-x)+1}$,
当x<0时,f-x)>0,则-1<f(x)=$\frac{-f(-x)}{f(-x)+1}=-1+\frac{1}{f(-x)+1}$<0,
∴x∈R时,f(x)=t∈(-1,+∞).
原不等式等价于:t2+2t-a≥at-5在t∈(-1,+∞)恒成立,
即tt2+2t+5≥(t+1)a⇒a≤$\frac{{t}^{2}+2t+5}{t+1}$.
g(t)=$\frac{{t}^{2}+2t+5}{t+1}=t+1+\frac{4}{t+1}≥4$,当t=1时取等号.
∴a≤4.
(3)由(2)可得f(x)∈(-1+∞),f(x+1)∈(-1+∞),
f(f(x))≥$\frac{7-f(x+1)}{1+f(x+1)}$⇒[1+f(x+1)]•f(f(x))≥7-f(x+1)⇒
f(x+1)•⇒[1+f(x+1)]•f(f(x))≥7-f(x+1)⇒
f(x+1)+f(x+1)•f(f(x))+f(f(x))≥7⇒f(x+1+f(x))≥7.
下面证明y=f(x)的单调性:
任取x1,x2∈R,且x1>x2,⇒f(x1-x2)>0,f(x2)>-1
则f(x1)-f(x2)=f(x1-x2+x2)-f(x2)=f(x1-x2)f(x2)+f(x1-x2)=f(x1-x2)[f(x2)+1]>0
所以函数 y=f(x)在R上单调递增,
∵f(3)═f(1)f(2)+f(2)+f(1)=7,
∴f(x+1+f(x))≥7⇒.f(x+1+f(x))≥f(3)⇒x+1+f(x)≥3
令F(x)=x+1+f(x),F(x)在R上单调递增,且F(1)=3
x+1+f(x)≥3?F(x)≥F(3)⇒x≥1,
所以原不等式解集为:[1,+∞).
点评 本题考查了抽象函数的单调性,及解抽象函数不等式的技巧,转化思想是关键,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,则 α∥β | B. | 若m∥α,α∥β,则 m∥β | ||
| C. | 若m?α,m⊥β,则 α⊥β | D. | 若m?α,α⊥β,则 m⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
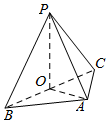 如图,在三棱锥P-ABC中,△PAB和△PAC均为边长是$\sqrt{2}$的正三角形,且∠BAC=90°,O为BC的中点.
如图,在三棱锥P-ABC中,△PAB和△PAC均为边长是$\sqrt{2}$的正三角形,且∠BAC=90°,O为BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com