
分析 根据题意,结合集合长度的定义,对集合A的子集分6种情况讨论,每种情况下分析符合条件的子集的数目,进而计算可得答案.
解答 解:根据题意,集合长度的定义,对集合A的子集分类讨论:
①、长度为0的子集,共6个:即{1}、{2}、{3}、{4}、{5}、{6},
②、长度为1的子集,必须为两个元素的集合,且其元素为相邻的两个自然数,共5个:
即{1,2}、{2,3}、{3,4}、{4,5}、{5,6},
③、长度为2的子集,即子集中最大最小元素差为2,
其中最小、最大元素有4种情况:即1、3,2、4,3、5,4、6;
每种情况有2个子集,
则共有8个子集,
④、长度为3的子集,即子集中最大最小元素差为3,
其中最小、最大元素有3种情况:即1、4,2、5,3、6;
每种情况有4个子集,
则共有12个子集,
⑤、长度为4的子集,即子集中最大最小元素差为4,
其中最小、最大元素有2种情况:即1、5,2、6;
每种情况有8个子集,
则共有16个子集,
⑥、长度为6的子集,即子集中最大最小元素差为5,
其中最小、最大元素有1种情况:即1、6;
则共有16个子集,
则U的所有非空子集的“长度”之和为:6×0+5×1+8×2+12×3+16×4+16×5=201;
故答案为:201.
点评 本题考查排列、组合的应用,涉及集合的子集的定义,关键是明确集合长度的定义,进而进行分类讨论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {2} | C. | {3,4} | D. | {5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
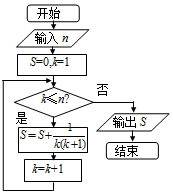
| A. | $\frac{5}{6}$ | B. | $\frac{6}{7}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{30}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com