
椭圆G:![]() 的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足
的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足![]()
(Ⅰ)求离心率e的取值范围;
(Ⅱ)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为![]() 求此时椭圆G的方程;(ⅱ)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点
求此时椭圆G的方程;(ⅱ)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点![]() 的直线对称?若能,求出k的取值范围;若不能,请说明理由
的直线对称?若能,求出k的取值范围;若不能,请说明理由
(1)![]() ;(2)(i)所求椭圆方程为
;(2)(i)所求椭圆方程为![]() ,(ⅱ)当
,(ⅱ)当![]() 时,A、B两点关于点P、Q的直线对称。
时,A、B两点关于点P、Q的直线对称。
(I)设M(x0,y0)
![]() ①
①
又![]() ②
②
由②得![]() 代入①式整理得
代入①式整理得 ![]()
又![]()
解得![]()
![]()
(Ⅱ)(i)当![]()
设H(x,y)为椭圆上一点,则
![]()
若0![]()
由![]() (舍去)
(舍去)
若b≥3,当y=-3时,|HN|2有最大值2b2+18
由2b2+18=50得b2=16
∴所求椭圆方程为![]()
(ii)设A(x1,y1),B(x2,y2),Q(x0,y0),则由
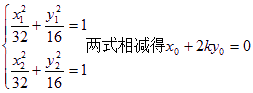 ③
③
又直线PQ⊥直线l ∴直线PQ方程为![]()
将点Q(x0,y0)代入上式得,![]() ④
④
由③④得Q![]()
(解1)而Q点必在椭圆内部 ![]()
由此得![]()
![]()
故当![]() 时A、B两点关于点P、Q的直线对称
时A、B两点关于点P、Q的直线对称
(解2)∴AB所在直线方程为![]()
由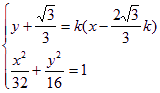 得
得
![]()
显然1+2k2≠0
而![]()
![]()
直线l与椭圆有两不同的交点A、B ∴△>0
解得![]()
![]()
故当![]() 时,A、B两点关于点P、Q的直线对称。
时,A、B两点关于点P、Q的直线对称。
(ii)另解;设直线l的方程为y=kx+b
由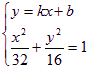 得
得
![]()
设A(x1,y1),B(x2,y2),Q(x0,y0),则
![]() ③
③
又直线PQ⊥直线l ∴直线PQ方程为![]()
将点Q(x0,y0)代入上式得,![]() ④
④
将③代入④![]() ⑤
⑤
∵x1,x2是(*)的两根
![]() ⑥
⑥
⑤代入⑥得![]()
∴当![]() 时,A、B两点关于点P、Q的直线对称。
时,A、B两点关于点P、Q的直线对称。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:山东省淄博市2011届高三第二次模拟数学理综试题 题型:044
椭圆G:![]() 的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为
的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为![]()
(1)求此时椭圆G的方程;
(2)设斜率为k(k≠0)的直线m与椭圆G相交于不同的两点E、F,Q为EF的中点,问E、F两点能否关于过点P(0,![]() )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
)、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设椭圆C1的方程为![]() (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=![]() ,且曲线C1与C2在第一象限内只有一个公共点P.
,且曲线C1与C2在第一象限内只有一个公共点P.
(1)试用a表示点P的坐标;
(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;
(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个. 设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川绵阳高中高三第二次诊断性考试理科数学试卷(解析版) 题型:解答题
已知椭圆C的两个焦点是(0,- )和(0,
)和(0, ),并且经过点
),并且经过点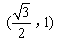 ,抛物线E的顶点在坐标原点,焦点F恰好是椭圆C的右顶点.
,抛物线E的顶点在坐标原点,焦点F恰好是椭圆C的右顶点.
(Ⅰ)求椭圆C和抛物线E的标准方程;
(Ⅱ)过点F作两条斜率都存在且互相垂直的直线l1、l2,l1交抛物线E于点A、B,l2交抛物线E于点G、H,求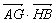 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆G:![]() 的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆 ,且点N(0,3)到椭圆上的点的最远距离为
的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆 ,且点N(0,3)到椭圆上的点的最远距离为![]()
(1)求此时椭圆G的方程;
(2)设斜率为k(k≠0)的直线m与椭圆G相交于不同的两点E、F,Q为EF的中点,问E、F两点能否关于过点![]() 的直线对称?若能,求出k的取值范围;若不能,请说明理由。
的直线对称?若能,求出k的取值范围;若不能,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
椭圆G:![]() 的两个焦点为F1、F2,短轴两端点B1、B2,已知
的两个焦点为F1、F2,短轴两端点B1、B2,已知
F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为![]()
(1)求此时椭圆G的方程;
(2)设斜率为k(k≠0)的直线m与椭圆G相交于不同的两点E、F,Q为EF的中点,问E、F两点能否关于过点P(0,![]() )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
)、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com