
已知函数f(x)=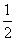 e2x-ax(a∈R,e为自然对数的底数).
e2x-ax(a∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性;
(2)若a=1,函数g(x)=(x-m)f(x)- e2x+x2+x在区间(0,+∞)上为增函数,求整数m的最大值.
e2x+x2+x在区间(0,+∞)上为增函数,求整数m的最大值.
解:(1)定义域为(-∞,+∞), f ′(x)=e2x-a,
当a≤0时,f ′(x)>0,所以f(x)在(-∞,+∞)上为增函数;
当a>0时,由f ′(x)=0得x=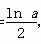
 ,且当x∈
,且当x∈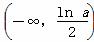 时, f ′(x)<0,
时, f ′(x)<0,
当x∈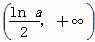 时f ′(x)>0,
时f ′(x)>0,
所以f(x)在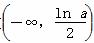 为减函数,在
为减函数,在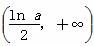 为增函数.
为增函数.
(2)当a=1时,g(x)=(x-m) 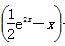 -
- e2x+x2+x,
e2x+x2+x,
若g(x)在区间(0,+∞)上为增函数,
则g′(x)=(x-m)(e2x-1)+x+1≥0在(0,+∞)恒成立,
即m≤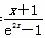 +x在(0,+∞)恒成立.
+x在(0,+∞)恒成立.
令h(x)=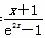 +x,x∈(0,+∞);
+x,x∈(0,+∞);
h′(x)=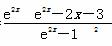 ,x∈(0,+∞);
,x∈(0,+∞);
令L(x)=e2x-2x-3,
可知L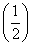 =e-4<0,L(1)=e2-5>0,
=e-4<0,L(1)=e2-5>0,
又当x∈(0,+∞)时L′(x)=2e2x-2>0,
所以函数L(x)=e2x-2x-3在x∈(0,+∞)只有一个零点,
设为α,即e2α=2α+3,且α∈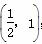 ;
;
由上可知当x∈(0,α)时L(x)<0,即h′(x)<0;
当x∈(α,+∞)时L(x)>0,即h′(x)>0,
所以h(x)=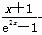 +x,x∈(0,+∞),有最小值h(α)=
+x,x∈(0,+∞),有最小值h(α)=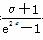 +α,
+α,
把e2α=2α+3代入上式可得h(α)=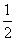 +α,又因为α∈
+α,又因为α∈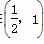 ,所以h(α)∈
,所以h(α)∈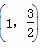 ,
,
又m≤h(x)恒成立,所以m≤h(α),又因为m为整数,
所以m≤1,所以整数m的最大值为1.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
已知函数f(x)=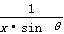 +ln x在[1,+∞)上为增函数,且θ∈(0,π),g(x)=tx-
+ln x在[1,+∞)上为增函数,且θ∈(0,π),g(x)=tx-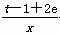 -ln x,t∈R.
-ln x,t∈R.
(1)求θ的值;
(2)当t=0时,求函数g(x)的单调区间和极大值;
(3)若在[1,e]上至少存在一个x0,使得g(x0)>f(x0)成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知x1,x2是函数f(x)=e-x-|ln x|的两个零点,则( )
A.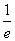 <x1x2<1 B.1<x1x2<e
<x1x2<1 B.1<x1x2<e
C.1<x1x2<10 D.e<x1x2<10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com