练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若函数f(x)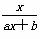＝ (a≠0)，f(2)＝1，又方程f(x)＝x有惟一解，求f(x)的解析式．


    解：由f(2)＝1得＝1，即2a＋b＝2；

    由f(x)＝x得＝x，变形得＝0，

    解此方程得x＝0或x＝，

    又因方程有惟一解，故＝0，

    解得b＝1，代入2a＋b＝2得a＝，

    所以f(x)＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    对算法的描述有：①对一类问题都有效；②对个别问题有效；③算法可以一步步地进行，每一步都有唯一的结果；④是一种通法，只要按部就班地做，总能得到结果，以上正确描述算法的有(　　)．

    A．1个                                           B．2个

    C．3个                                           D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题p：“存在x∈R，使4x＋2x＋1＋m＝0”，若“非p”是假命题，则实数m的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝，B＝，则A∩B＝(　　)

    A.   B．(2,3]C．[1,2)  D．(1,2)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝＋lg(2x＋1)的定义域是(　　)

    A.                          B.

    C.                             D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝4x2－mx＋5在[－2，＋∞)上递增，在(－∞，－2]上递减，则f(1)＝(　　)

    A．－7  B．1  C．17  D．25

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝的值域为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)是定义在R上的奇函数，且它的图象关于直线x＝1对称．

    (1)求证：f(x)是周期为4的周期函数；

    (2)若f(x)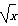＝ (0<x≤1)，求x∈[－5，－4]时，函数f(x)的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)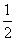＝e2x－ax(a∈R，e为自然对数的底数)．

    (1)讨论函数f(x)的单调性；

    (2)若a＝1，函数g(x)＝(x－m)f(x)－e2x＋x2＋x在区间(0，＋∞)上为增函数，求整数m的最大值．

    查看答案和解析>>

    同步练习册答案