




 -(n-1)2.
-(n-1)2. -2n+1
-2n+1


 -2n+1
-2n+1


 -2nqn
-2nqn

 …………………………12分
…………………………12分

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:不详 题型:解答题
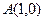 ,
,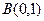 和互不相同的点
和互不相同的点 ,满足
,满足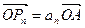
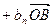
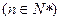 ,其中
,其中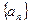 、
、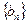 分别为等差数列和等比数列,
分别为等差数列和等比数列,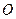 为坐标原点,
为坐标原点,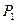 是线段
是线段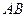 的中点.
的中点.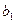 ,
,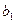 的值;
的值; 能否在同一条直线上?证明你的结论;
能否在同一条直线上?证明你的结论;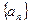 ,都能找到惟一的数列
,都能找到惟一的数列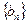 ,使得
,使得 都在一个指数函数的图象上.
都在一个指数函数的图象上.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
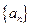 和
和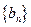 满足:
满足: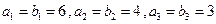 ,数列
,数列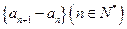 是等差数列,
是等差数列,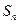 为数列
为数列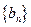 的前
的前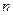 项和,且
项和,且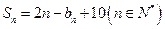 ,
,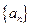 和
和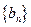 的通项公式;
的通项公式;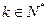 ,使
,使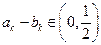 ?若存在,求出
?若存在,求出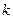 ,若不存在,说明理由。
,若不存在,说明理由。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com