
����Ŀ���ҹ���ˮ��Դ�ѷ��Ĺ��ң�Ϊ������Լ��ˮ��ij�д����̨һ��ˮ�����ߴ�ʩ���涨��ÿ����ÿ����ˮ��������5��ʱ��ÿ��ˮ���ջ�����1.3Ԫ��������5�ֶ�������6��ʱ���������ֵ�ˮ�Ѱ�������3����ȡ��������6�ֶ�������7��ʱ���������ֵ�ˮ�Ѱ�������5����ȡ��ij�˱�����ʵ����ˮ��Ϊ![]()
![]() �֣�Ӧ��ˮ��Ϊ
�֣�Ӧ��ˮ��Ϊ![]() Ԫ��
Ԫ��
��1����![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2�����������![]() �Ľ���ʽ��
�Ľ���ʽ��
���𰸡���1��5.2,8.45,13.65��2��f��x��=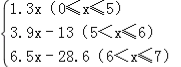
��������
�����������1������ÿһ����ÿ����ˮ��������5��ʱ��ÿ��ˮ���ջ�����1.3Ԫ����f��4��������������5�ֶ�������6��ʱ���������ֵ�ˮ�Ѽ���200%��f��5.5������2������ÿһ����ÿ����ˮ��������5��ʱ��ÿ��ˮ���ջ�����1.3Ԫ��������5�ֶ�������6��ʱ���������ֵ�ˮ�Ѽ���200%��������6�ֶ�������7��ʱ���������ֵ�ˮ�Ѽ���400%����Ϊ���Σ������ֶκ���ģ��
�����������1����������f��4��=4��1.3=5.2��
f��5.5��=5��1.3+0.5��3.9=8.45��
f��6.5��=5��1.3+1��3.9+0.5��6.5=13.65��
��2���������⣺
�ٵ�x��[0��5]ʱf��x��=1.3x
��������5�ֶ�������6��ʱ���������ֵ�ˮ�Ѽ���200%��
������x����5��6]ʱf��x��=1.3��5+��x��5����3.9=3.9x��13
�۵�x����6��7]ʱf��x��=6.5x��28
��f��x��=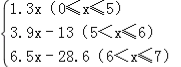 ��
��


 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������M��{1,3��a}��N��{2��a2}����M��N��{1,2,3,4,16}����a��ֵΪ�� ��
A.0
B.1
C.2
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ����������Ϊ
����������Ϊ![]() ����a2=2b��
����a2=2b��
��1������Բ�ķ��̣�
��2��ֱ��l��x��y+m=0����Բ����A��B���㣬�Ƿ����ʵ��m��ʹ�߶�AB���е���Բx2+y2=5�ϣ������ڣ����m��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪l��ƽ�����ֱ��mƽ���.�������ĸ����⣺
�٦��Φ�l��m���ڦ��ͦ�l��m����l��m���ͦ£���l��m���Φ�.
������ȷ�������ǣ� ��
A.�٢�
B.�ۢ�
C.�ڢ�
D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������X��Y���Ӧ��һ������Ϊ��10��1������11��3��2������11��8��3������12��5��4������13��5��������U��V���Ӧ��һ������Ϊ ��10��5������11��3��4������11��8��3������12��5��2������13��1����r1��ʾ����Y��X֮����������ϵ����r2��ʾ����V��U֮����������ϵ�������� ��
A��r2��r1��0 B��0��r2��r1
C��r2��0��r1 D��r2=r1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�ĵ����DZ߳�Ϊ1�������Σ�PA������ABCD��E��F�ֱ�ΪAB��PC���е㣮
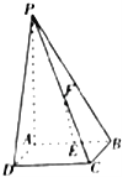
��������֤��EF��ƽ��PAD��
��������PA=2���������߶�EF���Ƿ���ڵ�Q��ʹ�ö����Q��AP��D������ֵΪ![]() �������ڣ�ȷ����Q��λ�ã��������ڣ���˵�����ɣ�
�������ڣ�ȷ����Q��λ�ã��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������ѧ�ؼ��Լ���������,�����漸������:��ϴ��ʢˮ2����;��ϴ��6����;��������������2����;���ù���ˮ�տ�10����;���������Ͳ˹�3����.���ϸ�������,������֮��,һ��ֻ�ܽ���һ������.С��Ҫ���������,����Ҫ��(����)
A. 13���� B. 14����
C. 15���� D. 23����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵԭ���뼫���꼫���غϣ�x���������뼫���غϣ�����֪����C�ļ����귽��Ϊ![]() ����F1��F2Ϊ�����ҽ��㣬ֱ��l�IJ�������Ϊ
����F1��F2Ϊ�����ҽ��㣬ֱ��l�IJ�������Ϊ ��tΪ������t��R����
��t������t��R����
������������C�ı����̺�ֱ��l����ͨ���̣�
����������PΪ����C�ϵĶ��㣬���P��ֱ��l����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��ֱ��
��ֱ��![]() ������
������![]() ���ڵ�
���ڵ�![]() ����������
����������![]() ���ڵ�
���ڵ�![]() .
.
��1����ʵ��![]() ��ֵ��
��ֵ��
��2��֤����������![]() ����������
����������![]() Ϊ������ʱ��
Ϊ������ʱ��![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com