
【题目】在![]() 中,内角
中,内角![]() 的对边分别为
的对边分别为![]() ,已知
,已知![]() .
.
(Ⅰ)求角![]() 的值;
的值;
(Ⅱ)若![]() ,当
,当![]() 取最小值时,求
取最小值时,求![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:方法一:(Ⅰ)利用正弦定理、诱导公式、两角和的正弦公式化简已知的式子,由内角的范围和特殊角的三角函数值求出角C;(Ⅱ)利用余弦定理列出方程,由条件和完全平方公式化简后,利用基本不等式求出c的最小值,由面积公式求出△ABC的面积;方法二:(Ⅰ)利用余弦定理化简已知的式子得到边的关系,由余弦定理求出cosC的值,由内角的范围和特殊角的三角函数值求出角C;(Ⅱ)利用余弦定理列出方程,结合条件消元后,利用一元二次函数的性质求出c的最小值,由面积公式求出△ABC的面积
试题解析:解法一(1)∵![]() ,∴
,∴![]() ……………………1分
……………………1分
∴![]() ……………2分
……………2分
即 ![]() ……………3分
……………3分
∴![]() 4分
4分
∵![]() ∴
∴ ![]() …………5分
…………5分
又∵![]() 是三角形的内角,∴
是三角形的内角,∴![]() ……6分
……6分
(2)由余弦定理得:![]() …………7分
…………7分
∵ ![]() ,故
,故![]() 8分
8分
∴ ![]() (当且仅当
(当且仅当![]() 时等号成立) ………10分
时等号成立) ………10分
∴![]() 的最小值为2,故
的最小值为2,故![]() ……12分
……12分
解法二:(1)∵![]() ,∴
,∴ ![]() ………1分
………1分
∴ ![]() ,即
,即 ![]() …………3分
…………3分
∴ ![]() …5分
…5分
又∵![]() 是三角形的内角,∴
是三角形的内角,∴![]() 6分
6分
(2)由已知,![]() ,即
,即![]() ,故:
,故:
![]() ……………8分
……………8分
∴ ![]() …………10分
…………10分
∴当![]() 时,
时,![]() 的最小值为2,故
的最小值为2,故![]() …………12分
…………12分


科目:高中数学 来源: 题型:
【题目】已知三次函数![]() ,下列命题正确的是 .
,下列命题正确的是 .
①函数![]() 关于原点
关于原点![]() 中心对称;
中心对称;
②以![]() ,
,![]() 两不同的点为切点作两条互相平行的切线,分别与
两不同的点为切点作两条互相平行的切线,分别与![]() 交于
交于![]() 两点,则这四个点的横坐标满足关系
两点,则这四个点的横坐标满足关系![]() ;
;
③以![]() 为切点,作切线与
为切点,作切线与![]() 图像交于点
图像交于点![]() ,再以点
,再以点![]() 为切点作直线与
为切点作直线与![]() 图像交于点
图像交于点![]() ,再以点
,再以点![]() 作切点作直线与
作切点作直线与![]() 图像交于点
图像交于点![]() ,则
,则![]() 点横坐标为
点横坐标为![]() ;
;
④若![]() ,函数
,函数![]() 图像上存在四点
图像上存在四点![]() ,使得以它们为顶点的四边形有且仅有一个正方形.
,使得以它们为顶点的四边形有且仅有一个正方形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如右表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
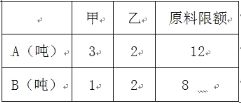
A.12万元 B.16万元
C.17万元 D.18万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() .
.
(1)求该方程表示一条直线的条件;
(2)当![]() 为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
(3)已知方程表示的直线![]() 在
在![]() 轴上的截距为-3,求实数
轴上的截距为-3,求实数![]() 的值;
的值;
(4)若方程表示的直线![]() 的倾斜角是45°,求实数
的倾斜角是45°,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
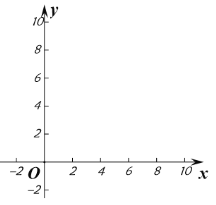
(1)在区间![]() 上画出函数
上画出函数![]() 的图象;
的图象;
(2)设集合![]() ,
,![]() .试判断集合
.试判断集合![]() 和
和![]() 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当![]() 时,求证:在区间
时,求证:在区间![]() 上,
上,![]() 的图象位于函数
的图象位于函数![]() 图象的上方.
图象的上方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班一次数学考试成绩频率分布直方图如图所示,数据分组依次为![]() ,已知成绩大于等于
,已知成绩大于等于![]() 分的人数为
分的人数为![]() 人,现采用分层抽样的方式抽取一个容量为
人,现采用分层抽样的方式抽取一个容量为![]() 的样本.
的样本.
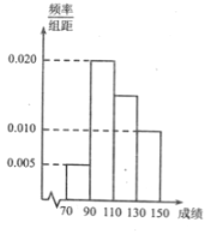
(1)求每个分组所抽取的学生人数;
(2)从数学成绩在![]() 的样本中任取
的样本中任取![]() 人,求恰有
人,求恰有![]() 人成绩在
人成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用![]() 的信息如下图。
的信息如下图。
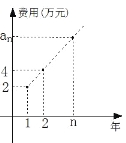
(Ⅰ)求![]() ;
;
(Ⅱ)引进这种设备后,第几年后该公司开始获利;
(Ⅲ)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com