
【题目】已知圆![]() 的圆心为原点,且与直线
的圆心为原点,且与直线![]() 相切.
相切.
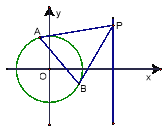
(1)求圆![]() 的方程;
的方程;
(2)点![]() 在直线
在直线![]() 上,过
上,过![]() 点引圆
点引圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】
试题分析:(1)由圆C与直线相切,得到圆心到直线的距离d=r,故利用点到直线的距离公式求出d的值,即为圆C的半径,又圆心为原点,写出圆C的方程即可;(2)由PA,PB为圆O的两条切线,根据切线的性质得到OA与AP垂直,OB与PB垂直,根据90°圆周角所对的弦为直径可得A,B在以OP为直径的圆上,设出P的坐标为(8,b),由P和O的坐标,利用线段中点坐标公式求出OP中点坐标,即为以OP为直径的圆的圆心坐标,利用两点间的距离公式求出OP的长,即为半径,写出以OP为直径的圆方程,整理后,由AB为两圆的公共弦,两圆方程相减消去平方项,得到弦AB所在直线的方程,可得出此直线方程过(2,0),得证
试题解析:(1)依题意得:圆![]() 的半径
的半径![]() ,……………2分
,……………2分
所以圆![]() 的方程为
的方程为![]() 。……………4分
。……………4分
(2)![]() 是圆
是圆![]() 的两条切线,
的两条切线,![]() 。
。
![]() 在以
在以![]() 为直径的圆上。……………6分
为直径的圆上。……………6分
设点![]() 的坐标为
的坐标为![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为![]() 。
。
![]() 以
以![]() 为直径的圆方程为
为直径的圆方程为![]() ……………8分
……………8分
化简得:![]()
![]() 为两圆的公共弦,
为两圆的公共弦,
![]() 直线
直线![]() 的方程为
的方程为![]() ……………10分
……………10分
所以直线![]() 恒过定点
恒过定点![]() 。……………12分
。……………12分


科目:高中数学 来源: 题型:
【题目】某市为增强市民的环境保护意识, 面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取![]() 名按年龄分组: 第
名按年龄分组: 第![]() 组
组![]() ,第2 组
,第2 组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示,
,得到的频率分布直方图如图所示,
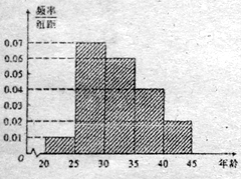
(1)若从第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名志愿者参与广场的宣传活动, 应从第
名志愿者参与广场的宣传活动, 应从第![]() 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(2)在(1)的条件下, 该县决定在这![]() 名志愿者中随机抽取
名志愿者中随机抽取![]() 名志愿者介绍宣传经验, 求第
名志愿者介绍宣传经验, 求第![]() 组至少有—名志愿者被抽中的概率.
组至少有—名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象上有一点列
的图象上有一点列![]() ,点
,点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() (
(![]() 且
且![]() ),
), ![]() .
.
(1)求证: ![]() 是等比数列,并求出数列
是等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设四边形![]() 的面积是
的面积是![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.
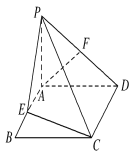
(1)求证:AF∥平面PCE.
(2)求证:平面PCD⊥平面PCE.
(3)若AD=2,CD=3,求点F到平面PCE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD的底面是边长为1的正方形,且侧棱PC⊥底面ABCD,且PC=2,E是侧棱PC上的动点

(1)求四棱锥P-ABCD的体积;
(2)证明:BD⊥AE。
(3)求二面角P-BD-C的正切值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015;已知函数f(x)=a2sin(ωx+φ)(ω>0,|φ|<![]() )的最小正周期是a1,且函数
)的最小正周期是a1,且函数![]() 的图象关于直线x=
的图象关于直线x=![]() 对称。
对称。

(Ⅰ)求函数![]() 表达式;
表达式;
(Ⅱ)已知△ABC中三边a,b,c对应角A,B,C,a=4,b=4![]() ,∠A=30°,求
,∠A=30°,求![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com