
【题目】设函数![]() .
.
(1)当![]() 时,设
时,设![]() ,求证:对任意的
,求证:对任意的![]() ,
,![]() ;
;
(2)当![]() 时,若对任意
时,若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)当![]() 时,原不等式等价于
时,原不等式等价于![]() .令
.令![]() ,求导后可知函数
,求导后可知函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,得证;(2)当
,得证;(2)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,令
,令![]() ,
,![]() ,对
,对![]() 求导后对
求导后对![]() 分成
分成![]() ,
,![]() 两类讨论,可求得实数
两类讨论,可求得实数![]() 的取值范围为
的取值范围为![]() .
.
试题解析:
(1)当![]() 时,
时,![]() ,
,
所以![]() 等价于
等价于![]() .
.
令![]() ,则
,则![]() ,可知函数
,可知函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,亦即
,亦即![]()
(2)当![]() 时,
时,![]() ,
,![]() .
.
所以不等式![]() 等价于
等价于![]() .
.
方法一:令![]() ,
,![]() ,
,
则![]() .
.
当![]() 时,
时,![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
所以根据题意,知有![]() ,∴
,∴![]()
当![]() 时,由
时,由![]() ,知函数
,知函数![]() 在
在![]() 上单调减;
上单调减;
由![]() ,知函数
,知函数![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() .
.
由条件知,![]() ,即
,即![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,所以
,所以![]() 与条件矛盾.
与条件矛盾.
综上可知,实数![]() 的取值范围为
的取值范围为![]() .
.
方法二:令![]() ,
,![]() ,
,
则![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,
,
所以![]() .
.
又![]() ,
,
显然当![]() 时,
时,![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() .
.
综上可知![]() 的取值范围为
的取值范围为![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】某班一次数学考试成绩频率分布直方图如图所示,数据分组依次为![]() ,已知成绩大于等于
,已知成绩大于等于![]() 分的人数为
分的人数为![]() 人,现采用分层抽样的方式抽取一个容量为
人,现采用分层抽样的方式抽取一个容量为![]() 的样本.
的样本.
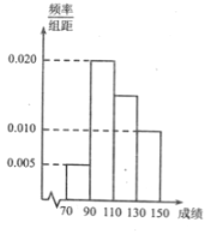
(1)求每个分组所抽取的学生人数;
(2)从数学成绩在![]() 的样本中任取
的样本中任取![]() 人,求恰有
人,求恰有![]() 人成绩在
人成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合I={1,2,3,4,5},选择I的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有
A.50种 B.49种 C.48种 D.47种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程,在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为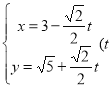 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极轴,以
为极轴,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的圆心到直线
的圆心到直线![]() 的距离;
的距离;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用![]() 的信息如下图。
的信息如下图。
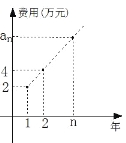
(Ⅰ)求![]() ;
;
(Ⅱ)引进这种设备后,第几年后该公司开始获利;
(Ⅲ)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程:
的方程:![]()
(1)求m的取值范围;
(2)若圆C与直线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的值
的值
(3)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com