
【题目】如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.
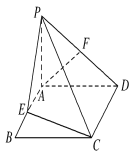
(1)求证:AF∥平面PCE.
(2)求证:平面PCD⊥平面PCE.
(3)若AD=2,CD=3,求点F到平面PCE的距离.
【答案】(1)详见解析(2)详见解析(3)![]()
【解析】
试题分析:(1)关键是证明AF与平面PEC内的一条直线平行,为此可取PC的中点G,论证AF∥EG;(2)可转化为证明线面垂直;(3)可以充分运用(2)的结论,结合线段比例关系求解点F到平面PCE的距离
试题解析:(1)证明:设M为PC中点,连接ME、MF.
则MF∥ ![]() CD,MF=
CD,MF= ![]() CD,AE∥
CD,AE∥![]() CD,AE=
CD,AE=![]() CD
CD
∴MF∥AE,MF=AE∴四边形AEMF为平行四边形.…………2分
∴AF∥ME,又∵ME平面PCE,AF平面PCE
∴AF∥平面PCE. …………4分
(2)证明:∵PA⊥平面ABCD,∠PDA=45°,
∴△PAD为等腰直角三角形,∵PF=FD,∴AF⊥PD,又∵PA⊥平面ABCD,PA平面PAD,
∴平面PAD⊥平面ABCD. …………6分
∵平面PAD∩平面ABCD=AD,
CD⊥AD,CD平面ABCD.
∴CD⊥平面PAD,∴AF⊥CD,
又∵PD∩CD=D,∴AF⊥平面PCD.
∵EM∥AF,
∴EM⊥平面PCD.
∵EM平面PCE,
∴平面PCE⊥平面PCD. …………8分
(3)过点F作FG⊥PC,交PC于G,∵平面PCE⊥平面PCD,∴FG⊥平面PCE,即FG为点F到平面PCE的距离.…………10分
在Rt△PCD中,PD=2![]() ,PC=
,PC=![]() .
.
∵△PFG∽△PCD,∴![]() ,
,
∴FG=![]() .…………12分
.…………12分


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如右表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
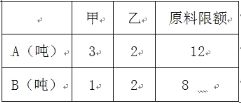
A.12万元 B.16万元
C.17万元 D.18万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)在区间![]() 上画出函数
上画出函数![]() 的图象;
的图象;
(2)设集合![]() ,
,![]() .试判断集合
.试判断集合![]() 和
和![]() 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当![]() 时,求证:在区间
时,求证:在区间![]() 上,
上,![]() 的图象位于函数
的图象位于函数![]() 图象的上方.
图象的上方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴正半轴上的圆
轴正半轴上的圆![]() 与直线
与直线![]() 相切,与
相切,与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
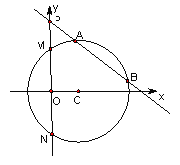
(1)求圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,若设点
,若设点![]() 为
为![]() 的重心,当
的重心,当![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班一次数学考试成绩频率分布直方图如图所示,数据分组依次为![]() ,已知成绩大于等于
,已知成绩大于等于![]() 分的人数为
分的人数为![]() 人,现采用分层抽样的方式抽取一个容量为
人,现采用分层抽样的方式抽取一个容量为![]() 的样本.
的样本.
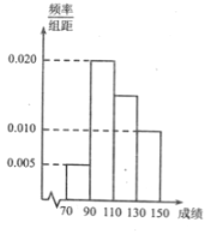
(1)求每个分组所抽取的学生人数;
(2)从数学成绩在![]() 的样本中任取
的样本中任取![]() 人,求恰有
人,求恰有![]() 人成绩在
人成绩在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com