
分析 由相位的终边落在y轴负半轴上,求得x值,得到使函数取得最小值的x值,并求得最小值;由相位的终边落在y轴正半轴上,求得x值,得到使函数取得最大值的x值,并求得最大值.
解答 解:当x-$\frac{π}{3}=-\frac{π}{2}+2kπ$,即x=2kπ-$\frac{π}{6},k∈Z$时,函数函数y=sin(x-$\frac{π}{3}$)-3有最小值-4;
当$x-\frac{π}{3}=\frac{π}{2}+2kπ$,即x=2kπ+$\frac{5π}{6}$,k∈Z时,函数函数y=sin(x-$\frac{π}{3}$)-3有最大值-2.
点评 本题考查y=Asin(ωx+φ)型函数的图象和性质,考查三角函数最值的求法,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在[-π,0]上是增函数,在[0,π]上是减函数 | |
| B. | 在[-$\frac{π}{2}$,$\frac{π}{2}$]上是增函数,在[-π,-$\frac{π}{2}$]和[$\frac{π}{2}$,π]上都是减函数 | |
| C. | 在[0,π]上是增函数,在[-π,0]上是减函数 | |
| D. | 在[$\frac{π}{2}$,π]和[-π,-$\frac{π}{2}$]上是增函数,在[-$\frac{π}{2}$,$\frac{π}{2}$]上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
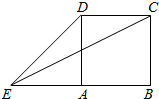 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则sin∠CED-cos∠CED=( )
如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则sin∠CED-cos∠CED=( )| A. | -$\frac{\sqrt{10}}{5}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{3\sqrt{10}}{10}$ | D. | $\frac{2\sqrt{10}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com