练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

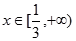    已知函数对任意的有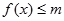恒成立，求实数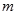的取值范围.

    解析试题分析：因为对任意的有恒成立,等价于:;而在上恒成立,所以在上是减函数,从而,故实数的取值范围为.
    考点：不等式的恒成立.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    实数满足，则的取值范围是          .

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    设偶函数f(x)对任意x∈R，都有，且当∈[－3，－2]时，，则的值是____________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    设函数是定义在R上的偶函数，且在区间[0，+∞)上单调递增，则满足不等式的的取值范围是                       ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知函数，，若，对，
     ，则      。

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    若函数的图像与轴有公共点，则的取值范围是_______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    某同学为研究函数f(x)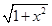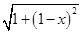＝＋(0≤x≤1)的性质，构造了如图所示的两个边长为1的正方形ABCD和BEFC，点P是边BC上的一个动点，设CP＝x，则AP＋PF＝f(x)．
    请你参考这些信息，推知函数f(x)的极值点是________；函数f(x)的值域是________．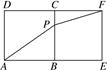

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    设函数在R上存在导数,对任意的有,且在上.若,则实数的取值范围           .

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知函数f(x)＝|2x－1|，a<b<c，且f(a)>f(c)>f(b)，则下列结论中，一定成立的是________．
    ①a<0，b<0，c<0; ②a<0，b≥0，c>0；③2－a<2c;  ④2a＋2c<2.

    查看答案和解析>>

    同步练习册答案