
分析 (1)由数量积的坐标运算得到f(x),利用辅助角公式化积,由周期公式求得周期,再由复合函数的单调性求得函数的减区间;
(2)由f(α)=$\frac{5}{3}$,求得$sin(2α+\frac{π}{6})=\frac{1}{3}$,得到cos2($α-\frac{π}{6}$)=$\frac{1}{3}$,展开二倍角的余弦求得cos(α-$\frac{π}{6}$)的值.
解答 解:(1)∵$\overrightarrow{m}$=(2cosx,1),$\overrightarrow{n}$=(cosx,$\sqrt{3}$sin2x),
∴f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$=$2co{s}^{2}x+\sqrt{3}sin2x$=$\sqrt{3}sin2x+cos2x+1$=$2sin(2x+\frac{π}{6})+1$.
∴f(x)的最小正周期T=$\frac{2π}{2}=π$,
由$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ$,得$\frac{π}{6}+kπ≤x≤\frac{2π}{3}+kπ,k∈Z$.
∴f(x)的单调递减区间为[$\frac{π}{6}+kπ,\frac{2π}{3}+kπ$],k∈Z;
(2)由f(α)=$\frac{5}{3}$,得$sin(2α+\frac{π}{6})=\frac{1}{3}$,从而sin[2($α-\frac{π}{6}$)+$\frac{π}{2}$]=$\frac{1}{3}$,
∴cos2($α-\frac{π}{6}$)=$\frac{1}{3}$.
即$2co{s}^{2}(α-\frac{π}{6})-1=\frac{1}{3}$,解得$cos(α-\frac{π}{6})=±\frac{\sqrt{6}}{3}$.
点评 本题考查平面向量的数量积运算,考查了y=Asin(ωx+φ)型函数的图象和性质,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
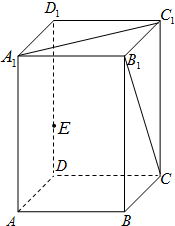 如图,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8,E为DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8,E为DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了了解中学生的体能状况,某校抽取了n名高一学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中第二小组频数为7.
为了了解中学生的体能状况,某校抽取了n名高一学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中第二小组频数为7.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com