
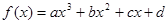
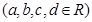 满足:
满足: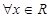 都有
都有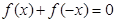 ,且
,且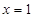 时,
时,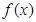 取极小值
取极小值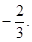
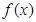 的解析式;
的解析式;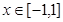 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;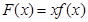 , 当
, 当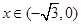 时,求函数
时,求函数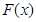 的最小值,并指出当
的最小值,并指出当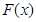 取最小值时相应的
取最小值时相应的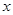 值.
值.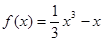
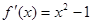 ,设:任意两数
,设:任意两数 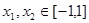 是函数
是函数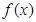 图像上两点的横坐标,则这两点处的切线的斜率分别是:
图像上两点的横坐标,则这两点处的切线的斜率分别是: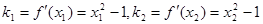 ,那么可以判定斜率之积不是-1,说明不能垂直
,那么可以判定斜率之积不是-1,说明不能垂直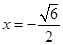 时,
时, 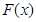 有最小值
有最小值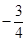
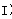 )因为,
)因为,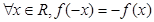 成立,所以:
成立,所以: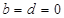 ,
,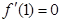 ,得
,得 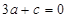 ,
,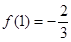 ,得
,得 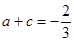
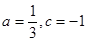 从而,函数解析式为:
从而,函数解析式为: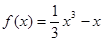 (4分)
(4分)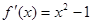 ,设:任意两数
,设:任意两数 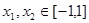 是函数
是函数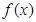 图像上两点的横坐标,则这两点处的切线的斜率分别是:
图像上两点的横坐标,则这两点处的切线的斜率分别是: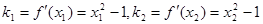
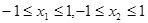 ,所以,
,所以,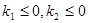 ,得:
,得: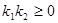 知:
知: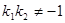
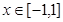 是函数
是函数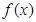 图像上任意两点处的切线不可能垂直 (8分)
图像上任意两点处的切线不可能垂直 (8分)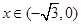 时,
时,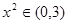 且
且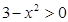 此时
此时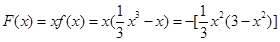
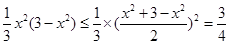 (11分)
(11分)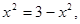 即
即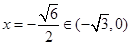 即,取等号,
即,取等号,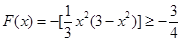
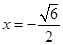 时,
时, 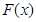 有最小值
有最小值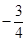 (13分)
(13分)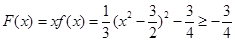 )
)

 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com