
(本小题满分14分)
求经过直线 与直线
与直线 的交点M,且分别满足下列条件的直线方程:
的交点M,且分别满足下列条件的直线方程:
(1)与直线 平行;
平行;
(2)与直线 垂直.
垂直.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:解答题
(本小题12分)
已知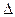 ABC的顶点C(5,1),AC边上的中线BM所在直线方程为
ABC的顶点C(5,1),AC边上的中线BM所在直线方程为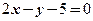 ,BC边上的高AH所在直线方程为
,BC边上的高AH所在直线方程为 ,求:
,求:
(1)顶点B的坐标;
(2)直线AC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知两直线 :
: 和
和 :
: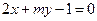 ,
,
(1)若 与
与 交于点
交于点 ,求
,求 的值;
的值;
(2)若 ,试确定
,试确定 需要满足的条件;
需要满足的条件;
(3)若l1⊥l2 ,试确定 需要满足的条件.
需要满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m.
(1) 求直线EF的方程(4 分 ).
(2) 应如何设计才能使草坪的占地面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com