
| A. | y2=2x | B. | y2=3x | C. | y2=4x | D. | y2=6x |
分析 求出双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程与抛物线y2=2px(p>0)的准线方程,进而求出A,B两点的坐标,再由双曲线的离心率为2,△AOB的面积为$\sqrt{3}$,列出方程,由此方程求出p的值,即可求出抛物线的方程.
解答 解:∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),
∴双曲线的渐近线方程是y=±$\frac{b}{a}$x
又抛物线y2=2px(p>0)的准线方程是x=-$\frac{p}{2}$,
故A,B两点的纵坐标分别是$\frac{pb}{2a}$、-$\frac{pb}{2a}$,
又由双曲线的离心率为2,所以$\frac{c}{a}$=2,则$\frac{b}{a}$=$\sqrt{3}$,
A,B两点的纵坐标分别是$\frac{\sqrt{3}p}{2}$、-$\frac{\sqrt{3}p}{2}$,
又△AOB的面积为$\sqrt{3}$,x轴是角AOB的角平分线
∴$\frac{1}{2}$×$\sqrt{3}p$×$\frac{p}{2}$=$\sqrt{3}$,得p=2,
∴抛物线的方程为y2=4x.
故选:C.
点评 本题考查圆锥曲线的共同特征,解题的关键是求出双曲线的渐近线方程,解出A,B两点的坐标,列出三角形的面积与离心率的关系也是本题的解题关键,有一定的运算量.


科目:高中数学 来源: 题型:选择题
| A. | 在这四个数中至少存在两个数x,y,满足sin(x-y)>$\frac{1}{2}$ | |
| B. | 在这四个数中至少存在两个数x,y,满足cos(x-y)≥$\frac{{\sqrt{3}}}{2}$ | |
| C. | 在四个数中至多存在两个数x,y,满足tan(x-y)<$\frac{{\sqrt{3}}}{3}$ | |
| D. | 在这四个数中至多存在两个数x,y,满足sin(x-y)≥$\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
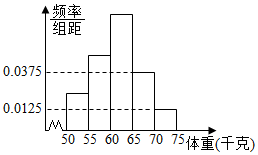 为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
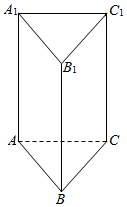 三棱柱ABC-A1B1C1中,底面ABC为等边三角形,AB=2,C1C⊥底面ABC,BC1与底面ABC所成角为45°,则此三棱柱体积是2$\sqrt{3}$.
三棱柱ABC-A1B1C1中,底面ABC为等边三角形,AB=2,C1C⊥底面ABC,BC1与底面ABC所成角为45°,则此三棱柱体积是2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
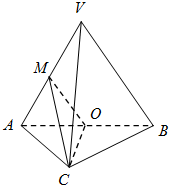 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com