
| A. | 在这四个数中至少存在两个数x,y,满足sin(x-y)>$\frac{1}{2}$ | |
| B. | 在这四个数中至少存在两个数x,y,满足cos(x-y)≥$\frac{{\sqrt{3}}}{2}$ | |
| C. | 在四个数中至多存在两个数x,y,满足tan(x-y)<$\frac{{\sqrt{3}}}{3}$ | |
| D. | 在这四个数中至多存在两个数x,y,满足sin(x-y)≥$\frac{{\sqrt{3}}}{3}$ |
分析 由题意可得,在这四个数中至少存在两个数x,y,满足|x-y|≤$\frac{π}{6}$,从而得出结论.
解答 解:设x1,x2,x3,x4∈(0,$\frac{π}{2}$),而(0,$\frac{π}{2}$)的区间长度为$\frac{π}{2}$,
在这四个数x1,x2,x3,x4中,设其中两个相邻的最靠近的数为x、y,
则|x-y|的最大值为$\frac{\frac{π}{2}}{3}$=$\frac{π}{6}$,故在这四个数中至少存在两个数x,y,满足|x-y|≤$\frac{π}{6}$,
∴cos(x-y)≥$\frac{{\sqrt{3}}}{2}$,
故选:B.
点评 本题主要考查余弦函数的图象特征,属于基础题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
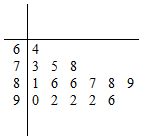 为了解某生产线的运行情况,从该生产线上随机抽取了15件产品进行检测,得分低于85分的为不合格品,得分不低于85分的为合格品.该批产品检测得分情况如下:
为了解某生产线的运行情况,从该生产线上随机抽取了15件产品进行检测,得分低于85分的为不合格品,得分不低于85分的为合格品.该批产品检测得分情况如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5x-12y+38=0或3x-4y+10=0 | B. | 12x-5y+4=0或3x-4y+10=0 | ||
| C. | 5x-12y+38=0或x=2 | D. | 3x-4y+10=0或x=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)的一条对称轴方程为x=$\frac{π}{12}$ | B. | g(x)的值域为[-$\sqrt{2}$,$\sqrt{2}$] | ||
| C. | 在(0,π)上单调递减 | D. | 关于点($\frac{13π}{12}$,$\frac{1}{2}$)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{2}$ | B. | -$\frac{2}{5}$ | C. | $\frac{2}{5}$ | D. | $±\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=2x | B. | y2=3x | C. | y2=4x | D. | y2=6x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com