
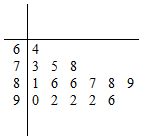
 为了解某生产线的运行情况,从该生产线上随机抽取了15件产品进行检测,得分低于85分的为不合格品,得分不低于85分的为合格品.该批产品检测得分情况如下:
为了解某生产线的运行情况,从该生产线上随机抽取了15件产品进行检测,得分低于85分的为不合格品,得分不低于85分的为合格品.该批产品检测得分情况如下:分析 (Ⅰ)由茎叶图能求出该组数据的中位数和众数,抽取的15件产品中,合格品有10件,由此能估计该条生产线所生产的产品为合格品的概率.
(Ⅱ)若生产该产品150件,则有50件不合格品,100件合格品,由此能求出生产150件上述产品平均一件的利润.
解答 解:(Ⅰ)由已知得该组数据的中位数为87,众数为92,
抽取的15件产品中,合格品有10件,
由此估计该条生产线所生产的产品为合格品的概率为p=$\frac{10}{15}$=$\frac{2}{3}$.…(5分)
(Ⅱ)由(Ⅰ)得若生产该产品150件,则有50件不合格品,100件合格品,
∴生产150件上述产品平均一件的利润为:
$\frac{1}{150}$×(100×270-50×90)=150元.…(12分)
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意茎叶图的性质及等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}$+y2=1 | B. | $\frac{x^2}{3}$+y2=1 | C. | $\frac{x^2}{2}$+y2=1 | D. | $\frac{x^2}{4}$+$\frac{y^2}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6±2$\sqrt{35}$ | B. | 2±$\sqrt{35}$ | C. | 8±$\sqrt{35}$ | D. | 1±$\sqrt{35}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
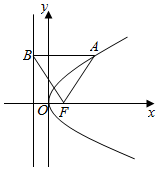 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若△ABF为等边三角形,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若△ABF为等边三角形,则抛物线的标准方程是( )| A. | y2=$\frac{1}{2}$x | B. | y2=x | C. | y2=2x | D. | y2=4x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | (0,2] | C. | (2,3) | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在这四个数中至少存在两个数x,y,满足sin(x-y)>$\frac{1}{2}$ | |
| B. | 在这四个数中至少存在两个数x,y,满足cos(x-y)≥$\frac{{\sqrt{3}}}{2}$ | |
| C. | 在四个数中至多存在两个数x,y,满足tan(x-y)<$\frac{{\sqrt{3}}}{3}$ | |
| D. | 在这四个数中至多存在两个数x,y,满足sin(x-y)≥$\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com