
分析 由已知得每个人接受挑战的概率是$\frac{1}{2}$,不接受挑战的概率也是$\frac{1}{2}$,由此能求出这3个人中至少有2个人接受挑战的概率.
解答 解:∵每个人接受挑战和不接受挑战是等可能的,
∴每个人接受挑战的概率是$\frac{1}{2}$,不接受挑战的概率也是$\frac{1}{2}$,
设事件M为“这3个C人中至少有2个人接受挑战”,
则P(M)=${C}_{3}^{2}•(\frac{1}{2})^{2}•\frac{1}{2}+{C}_{3}^{3}•(\frac{1}{2})^{3}$=$\frac{1}{2}$.
点评 本题主要考查古典概型的概率问题,关键是掌握服从超几何分布的概率公式,属于基础题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
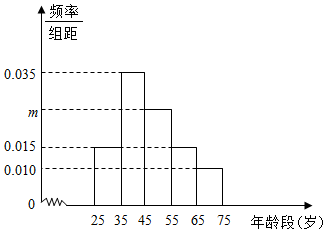 2016年2月,国务院发布的《关于进一步加强城市规划建设管理工作的若干意见》中提到“原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院要逐步打开”,济南某新闻媒体对某一小区100名不同年龄段的居民进行调查,如图是各年龄段支持以上做法的人数的频率分布直方图.
2016年2月,国务院发布的《关于进一步加强城市规划建设管理工作的若干意见》中提到“原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院要逐步打开”,济南某新闻媒体对某一小区100名不同年龄段的居民进行调查,如图是各年龄段支持以上做法的人数的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{12}{5}$ | B. | $\frac{12}{5}$ | C. | -$\frac{5}{12}$ | D. | ±$\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
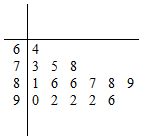 为了解某生产线的运行情况,从该生产线上随机抽取了15件产品进行检测,得分低于85分的为不合格品,得分不低于85分的为合格品.该批产品检测得分情况如下:
为了解某生产线的运行情况,从该生产线上随机抽取了15件产品进行检测,得分低于85分的为不合格品,得分不低于85分的为合格品.该批产品检测得分情况如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com