
分析 (Ⅰ)当n=1时,求得a1=35;n>1时,再将n换为n-1,两式相除,可得an=40-5n;检验可得数列的通项公式;
(Ⅱ)运用等差数列的求和公式,求得Tn=|15(11-2n)|=15|11-2n|,讨论单调性,可得最小值.
解答 解:(Ⅰ)当n=1时,${2^{a_1}}={2^{35}}$,即有a1=35,
n≥2时,${2^{a_1}}•{2^{a_2}}…{2^{a_n}}={2^{\frac{{75n-5{n^2}}}{2}}}$,
${2^{a_1}}•{2^{a_2}}…{2^{{a_{n-1}}}}={2^{\frac{{75({n-1})-5{{({n-1})}^2}}}{2}}}$,
两式相除得,2${\;}^{{a}_{n}}$=2${\;}^{\frac{75n-5{n}^{2}}{2}-\frac{75(n-1)-5(n-1)^{2}}{2}}$,
化简得,${2^{a_n}}={2^{40-5n}}$,即an=40-5n;
又a1=35满足上式,所以an=40-5n(n∈N*);
(Ⅱ)由(Ⅰ)得,${a_n}+{a_{n+1}}+…+{a_{n+5}}=\frac{{6({{a_n}+{a_{n+5}}})}}{2}=15({11-2n})$,
所以Tn=|15(11-2n)|=15|11-2n|,
当1≤n≤5时,Tn递减;n≥6,n∈N*,Tn递增,
则当n=5,或n=6时,|Tn|的最小值为15.
点评 本题考查数列的通项公式的求法,注意运用下标变换相除,考查数列的最值的求法,注意运用数列的单调性,考查化简整理的运算能力,属于中档题.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若“p∨q”为假命题,则p,q均为假命题 | |
| B. | “a>b”是“ac2>bc2”的充分不必要条件 | |
| C. | 命题:“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0” | |
| D. | 命题:“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在这四个数中至少存在两个数x,y,满足sin(x-y)>$\frac{1}{2}$ | |
| B. | 在这四个数中至少存在两个数x,y,满足cos(x-y)≥$\frac{{\sqrt{3}}}{2}$ | |
| C. | 在四个数中至多存在两个数x,y,满足tan(x-y)<$\frac{{\sqrt{3}}}{3}$ | |
| D. | 在这四个数中至多存在两个数x,y,满足sin(x-y)≥$\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
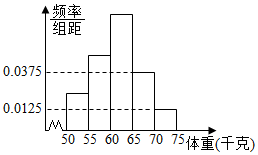 为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com