
分析 (Ⅰ)根据盒子中装有形状大小相同的5张卡片,上面分别标有数字1,2,3,4,5,可以写出所有可能的结果,从而求出甲乙所抽卡片上的数字之和为偶数的概率;
(Ⅱ)确定剩下的三边长包含的基本事件,剩下的三张卡片上的数字作为边长能构成三角形的基本事件,即可求出能构成三角形的概率.
解答 解:(Ⅰ)甲乙两人分别从盒子中随机不放回的各抽取一张,基本事件有:
(1,2),(1,3),(1,4),(1,5),(2,1),(2,3),(2,4),
(2,5),(3,1),(3,2),(3,4),(3,5),(4,1),(4,2),
(4,3),(4,5),(5,1),(5,2),(5,3),(5,4)共20个
设“甲、乙两人所抽取卡片上的数字之和为偶数”为事件A,
则事件A包含的基本事件有:(1,3),(1,5),(2,4),(3,1),(3,5),(4,2),(5,1),(5,3),共8个.
所以$P(A)=\frac{8}{20}=\frac{2}{5}$.
(Ⅱ)以盒子中剩下的三张卡片上的数字作为线段长度所包含的基本事件有:
{1,2,3},{1,2,4},{1,2,5},{1,3,4},{1,3,5},{1,4,5},{2,3,4},{2,3,5},{2,4,5},{3,4,5},共10个.
设“以盒子中剩下的三张卡片上的数字作为线段长度,求以这三条线段为边可以构成三角形”为事件B,
则事件B包含的基本事件有{2,3,4},{2,4,5},{3,4,5},共3个.
所以$P(B)=\frac{3}{10}$.
点评 本题考查了古典概型概率的问题,关键是不重不漏的列举所有的基本事件,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
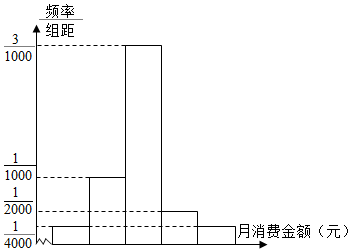 某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:
某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}$+y2=1 | B. | $\frac{x^2}{3}$+y2=1 | C. | $\frac{x^2}{2}$+y2=1 | D. | $\frac{x^2}{4}$+$\frac{y^2}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com