
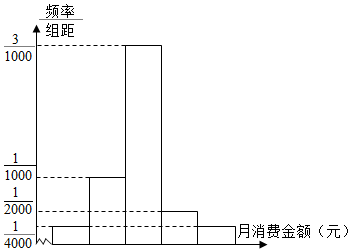
 某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:
某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:分析 (Ⅰ)由频率分布直方图能求出学生月消费的平均数.
(Ⅱ)(ⅰ)月消费值落入区间[200,400)、[400,800)、[800,1200]的频率分别为0.05、0.80、0.15,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
(ii)先求出服务部的月利润,再求出受助学生人数,由此能求出每个受助学生每月可获得多少元.
解答 解:(Ⅰ)由频率分布直方图得学生月消费的平均数:
$\overline x=(\frac{1}{4000}×300+\frac{1}{1000}×500+\frac{3}{1000}×700+\frac{1}{2000}×900+\frac{1}{4000}×1100)×200$…(2分)
=680…(4分)
(Ⅱ)(ⅰ)月消费值落入区间[200,400)、[400,800)、[800,1200]的频率分别为0.05、0.80、0.15,
∴P(ξ=20)=0.05,
P(ξ=40)=0.80,
P(ξ=80)=0.15,
∴ξ的分布列为:
| ξ | 20 | 40 | 80 |
| P | 0.05 | 0.80 | 0.15 |
点评 本小题主要考查频率分布直方图、平均数、随机变量的分布列及数学期望等基础知识,考查运算求解能力、数据处理能力、应用意识,考查分类与整合思想、必然与或然思想、化归与转化思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com