
分析 (Ⅰ)利用抛物线定义,求出p,即可求出求抛物线E的方程,A代入抛物线方程,即可求出A点的坐标;
(Ⅱ)求出直线l的方程,代入y2=4x整理得2x2-9x+8=0,利用弦长公式求出|MN|.
解答 解:(Ⅰ)由题意和抛物线定义得$2+\frac{p}{2}=3$,解得p=2,
故抛物线E的方程为y2=4x,…(3分)
因为点A在抛物线E上,所以m2=8,又m>0,
故$m=2\sqrt{2}$,于是$A(2,2\sqrt{2})$.…(6分)
(Ⅱ)由(I)知F(1,0),$A(2,2\sqrt{2})$,故直线AF的斜率为$2\sqrt{2}$
由题意得直线l的方程为$y=2\sqrt{2}(x-2)$,…(8分)
把它代入y2=4x整理得2x2-9x+8=0,△=(-9)2-4×2×8>0
设M(x1,y1),N(x2,y2),则${x_1}+{x_2}=\frac{9}{2},{x_1}{x_2}=4$…(10分)
故$|{MN}|=\sqrt{1+{k^2}}•|{{x_2}-{x_1}}|=\sqrt{1+{{(2\sqrt{2})}^2}}•\sqrt{{{(\frac{9}{2})}^2}-4×4}=\frac{{3\sqrt{17}}}{2}$…(12分)
点评 本题考查抛物线的方程与定义,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Sk+$\frac{1}{2k+1}$ | B. | Sk+$\frac{1}{2k}$+$\frac{1}{2k+1}$ | ||
| C. | Sk+$\frac{1}{2k}$+$\frac{1}{2k+1}$-$\frac{1}{k+2}$ | D. | Sk-$\frac{1}{2k}$-$\frac{1}{2k+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
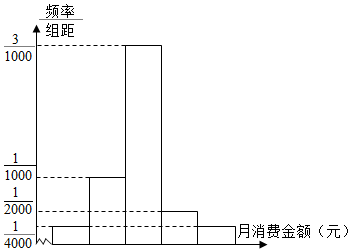 某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:
某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com