
分析 (Ⅰ)由点到直线的距离公式求出a值,得到直线m的方程,再联立直线方程与圆的方程,求得B的坐标,进一步求得直线l的方程;
(Ⅱ)设A,B两点的纵坐标分别为y1,y2,由圆的方程求出D的坐标,设出AB所在直线方程,联立直线方程与圆的方程,化为关于y的一元二次方程,利用根与系数的关系求出A,B两点纵坐标差的绝对值,代入三角形面积公式,换元后利用基本不等式求得最值.
解答 解:(Ⅰ)由圆C:x2+y2-4x-1=0,得(x-2)2+y2=5,
∴圆心坐标为(2,0),半径为$\sqrt{5}$.
直线m与圆C相切,得$\frac{|3a+2|}{\sqrt{{a}^{2}+4}}=\sqrt{5}$,
化简得:a2+3a-4=0,解得a=1或a=-4,
由于a>0,故a=1,
∴直线m:x-2y+3=0.
联立$\left\{\begin{array}{l}{x-2y+3=0}\\{{x}^{2}+{y}^{2}-4x-1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
故直线m与圆相切于点B(1,2),得l:y=2x;
(Ⅱ)设A,B两点的纵坐标分别为y1,y2,
求得圆C与x轴正半轴交点D($2+\sqrt{5}$,0),
则${S}_{△ABD}=\frac{1}{2}(2+\sqrt{5})(|{y}_{1}|+|{y}_{2}|)$=$\frac{1}{2}(2+\sqrt{5})|{y}_{1}-{y}_{2}|$,
设AB方程为x=ty,
由$\left\{\begin{array}{l}{x=ty}\\{{x}^{2}+{y}^{2}-4x-1=0}\end{array}\right.$,消元得(t2+1)y2-4ty-1=0,
$|{y}_{1}-{y}_{2}|=\frac{\sqrt{△}}{1+{t}^{2}}$=$\frac{\sqrt{20{t}^{2}+4}}{1+{t}^{2}}=2\sqrt{\frac{5{t}^{2}+1}{({t}^{2}+1)^{2}}}$.
设m=5t2+1,
则$|{{y_1}-{y_2}}|=2\sqrt{\frac{25m}{{{m^2}+8m+16}}}=2\sqrt{\frac{25}{{m+8+\frac{16}{m}}}}$$≤\frac{5}{2}$,当且仅当m=4时取等号.
故△ABD面积最大值为$\frac{5}{4}(2+\sqrt{5})$.
点评 本题考查圆的切线方程,考查了点到直线距离公式的应用,考查直线与圆位置关系的应用,体现了数学转化思想方法,是中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≥1 | B. | k>1 | C. | k≥2 | D. | k>2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲校 | 乙校 | 丙校 | |
| 男生 | 97 | 90 | x |
| 女生 | 153 | y | z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
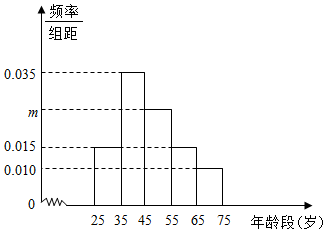 2016年2月,国务院发布的《关于进一步加强城市规划建设管理工作的若干意见》中提到“原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院要逐步打开”,济南某新闻媒体对某一小区100名不同年龄段的居民进行调查,如图是各年龄段支持以上做法的人数的频率分布直方图.
2016年2月,国务院发布的《关于进一步加强城市规划建设管理工作的若干意见》中提到“原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院要逐步打开”,济南某新闻媒体对某一小区100名不同年龄段的居民进行调查,如图是各年龄段支持以上做法的人数的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com