
分析 运用分析法证明,通过两边平方和不等式的性质,化简整理,再由均值不等式即可得证.
解答 证明:要证$\sqrt{a+\frac{1}{a}}$-$\sqrt{2}$≥$\sqrt{a}$+$\frac{1}{{\sqrt{a}}}$-2,
只需证$\sqrt{a+\frac{1}{a}}$+2≥$\sqrt{a}$+$\frac{1}{\sqrt{a}}$+$\sqrt{2}$,
两边平方,即为a+$\frac{1}{a}$+4+4$\sqrt{a+\frac{1}{a}}$≥a+$\frac{1}{a}$+2+2$\sqrt{2}$($\sqrt{a}$+$\frac{1}{{\sqrt{a}}}$)+2,
即证$\sqrt{a+\frac{1}{a}}$≥$\frac{\sqrt{2}}{2}$($\sqrt{a}$+$\frac{1}{{\sqrt{a}}}$),
两边平方可得a+$\frac{1}{a}$≥$\frac{1}{2}$(a+$\frac{1}{a}$+2),
即证a+$\frac{1}{a}$≥2,由a>0,a+$\frac{1}{a}$≥2$\sqrt{a•\frac{1}{a}}$=2,上式显然成立.
故原不等式成立.
点评 本题考查不等式的证明,注意运用分析法证明,通过平方法和不等式的性质,及均值不等式,考查推理能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 第一排 | 明文字母 | A | B | C |
| 密码数字 | 11 | 12 | 13 | |
| 第二排 | 明文字母 | E | F | G |
| 密码数字 | 21 | 22 | 23 | |
| 第三排 | 明文字母 | M | N | P |
| 密码数字 | 1 | 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
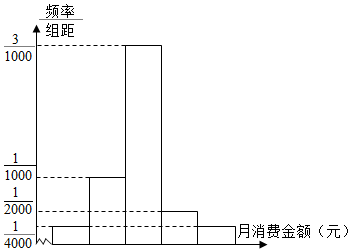 某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:
某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com