
分析 (1)由a+$\frac{{b}^{2}}{a}$≥2$\sqrt{a•\frac{{b}^{2}}{a}}$=2b,b+$\frac{{c}^{2}}{b}$≥2c,c+$\frac{{a}^{2}}{c}$≥2a,累加即可得证;
(2)运用作差法,结合三元均值不等式,即可得证.
解答 证明:(1)由a,b,c>0,可得a+$\frac{{b}^{2}}{a}$≥2$\sqrt{a•\frac{{b}^{2}}{a}}$=2b,
b+$\frac{{c}^{2}}{b}$≥2c,c+$\frac{{a}^{2}}{c}$≥2a,
相加可得(a+b+c)+($\frac{{b}^{2}}{a}$$+\frac{{c}^{2}}{b}$$+\frac{{a}^{2}}{c}$)≥2(a+b+c),
即为$\frac{{b}^{2}}{a}$$+\frac{{c}^{2}}{b}$$+\frac{{a}^{2}}{c}$≥a+b+c(当且仅当a=b=c取得等号);
(2)3($\frac{a+b+c}{3}$-$\root{3}{abc}$)-2($\frac{a+b}{2}$-$\sqrt{ab}$)
=c+2$\sqrt{ab}$-3$\root{3}{abc}$=c+$\sqrt{ab}$+$\sqrt{ab}$-3$\root{3}{abc}$
≥3$\root{3}{abc}$-3$\root{3}{abc}$=0,
可得2($\frac{a+b}{2}$-$\sqrt{ab}$)≤3($\frac{a+b+c}{3}$-$\root{3}{abc}$)(当且仅当a=b=c取得等号).
点评 本题考查不等式的证明,注意运用均值不等式,考查累加法和作差法的运用,以及推理运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第一排 | 明文字母 | A | B | C |
| 密码数字 | 11 | 12 | 13 | |
| 第二排 | 明文字母 | E | F | G |
| 密码数字 | 21 | 22 | 23 | |
| 第三排 | 明文字母 | M | N | P |
| 密码数字 | 1 | 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
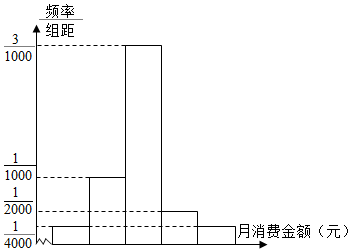 某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:
某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com