
分析 由条件化简可得原不等式即为n${\;}^{\frac{1}{m}-a}$>m${\;}^{\frac{1}{n}-a}$,可得lnn${\;}^{\frac{1}{m}-a}$>lnm${\;}^{\frac{1}{n}-a}$,可得$\frac{lnm}{\frac{1}{m}-a}$<$\frac{lnn}{\frac{1}{n}-a}$,设f(x)=$\frac{lnx}{\frac{1}{x}-a}$,求出导数,由题意可得f(x)在(0,$\frac{1}{a}$)递减,再由f′(x)≤0恒成立,即可求得a的最小值.
解答 解:由0<n<m<$\frac{1}{a}$,
$\frac{\root{m}{n}}{\root{n}{m}}$>$\frac{{n}^{a}}{{m}^{a}}$即为$\frac{{n}^{\frac{1}{m}}}{{n}^{a}}$>$\frac{{m}^{\frac{1}{n}}}{{m}^{a}}$,
即有n${\;}^{\frac{1}{m}-a}$>m${\;}^{\frac{1}{n}-a}$,
可得lnn${\;}^{\frac{1}{m}-a}$>lnm${\;}^{\frac{1}{n}-a}$,
即有($\frac{1}{m}$-a)lnn>($\frac{1}{n}$-a)lnm恒成立,
由$\frac{1}{n}$-a>$\frac{1}{m}$-a>0,可得
$\frac{lnm}{\frac{1}{m}-a}$<$\frac{lnn}{\frac{1}{n}-a}$,
设f(x)=$\frac{lnx}{\frac{1}{x}-a}$,则f′(x)=$\frac{\frac{1}{x}(\frac{1}{x}-a)+lnx•\frac{1}{{x}^{2}}}{(\frac{1}{x}-a)^{2}}$,
由0<n<m<$\frac{1}{a}$,可得f(x)在(0,$\frac{1}{a}$)递减,
可得f′(x)≤0恒成立,即为
$\frac{1}{x}$($\frac{1}{x}$-a)+lnx•$\frac{1}{{x}^{2}}$≤0,
即有a≥$\frac{1+lnx}{x}$恒成立,
由g(x)=$\frac{1+lnx}{x}$的导数为g′(x)=$\frac{1-(1+lnx)}{{x}^{2}}$=-$\frac{lnx}{{x}^{2}}$,
当$\frac{1}{a}$≤1即a≥1时,g(x)递增,a≥$\frac{1+ln\frac{1}{a}}{\frac{1}{a}}$,
即1≥1-lna,显然成立;
当$\frac{1}{a}$≥1即0<a≤1时,可得x=1处取得最大值1,即a≥1,
显然a=1不恒成立.
综上可得a的最小值为1.
故答案为:1.
点评 本题考查不等式恒成立问题的解法,注意运用转化思想和构造函数法,运用导数判断单调性,考查化简整理的运算能力,属于难题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
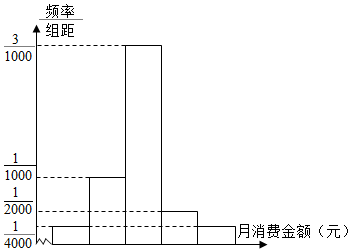 某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:
某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:| 阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
| 月用水量范围(单位:立方米) | (0,10] | (10,15] | (15,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com