
| A. | 5x-12y+38=0或3x-4y+10=0 | B. | 12x-5y+4=0或3x-4y+10=0 | ||
| C. | 5x-12y+38=0或x=2 | D. | 3x-4y+10=0或x=2 |
分析 设所求圆的方程为:(x2+y2-4)+a(x+y-1)=0即x2+y2+ax+ay-4-a=0,由圆心为(-2,-2)求出a的值,即可求出圆的半径,然后讨论:当过点(2,4)的直线斜率不存在时,方程是x=2,通过验证圆心到直线的距离,得到x=2符合题意;当过点(2,4)的直线斜率存在时,设直线方程为y-4=k(x-2),根据圆心到直线的距离等于半径4,建立关于k的方程,解之得k,进而得到直线的方程.最后综合可得答案.
解答 解:设所求圆的方程为:(x2+y2-4)+a(x+y-1)=0即x2+y2+ax+ay-4-a=0,
∵圆心为(-2,-2),
∴a=4.
∴圆的方程为x2+y2+4x+4y-8=0,即(x+2)2+(y+2)2=16.
则圆心为:(-2,-2),半径为4.
(1)当过点(2,4)的直线垂直于x轴时,
此时直线斜率不存在,方程是x=2,
∵圆心(-2,-2)到直线的距离为d=4=r,
∴直线x=2符合题意;
(2)当过点(2,4)的直线不垂直于x轴时,设直线方程为y-4=k(x-2)
即kx-y-2k+4=0,
由点到直线的距离公式可得:$\frac{|-2k+2-2k+4|}{\sqrt{{k}^{2}+1}}=4$,
解得:k=$\frac{5}{12}$.
∴切线方程为:5x-12y+38=0.
综上切线方程为:5x-12y+38=0或x=2.
故选:C.
点评 本题考查圆的切线方程,考查了求过圆外一个定点的圆的切线方程的问题,考查了直线与圆的位置关系、点到直线的距离公式等知识点,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某次数学小测验中(满分100分),某班50名学生得分如下面的频率分布直方图所示:
某次数学小测验中(满分100分),某班50名学生得分如下面的频率分布直方图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在这四个数中至少存在两个数x,y,满足sin(x-y)>$\frac{1}{2}$ | |
| B. | 在这四个数中至少存在两个数x,y,满足cos(x-y)≥$\frac{{\sqrt{3}}}{2}$ | |
| C. | 在四个数中至多存在两个数x,y,满足tan(x-y)<$\frac{{\sqrt{3}}}{3}$ | |
| D. | 在这四个数中至多存在两个数x,y,满足sin(x-y)≥$\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨(¬q) | B. | p∨q | C. | (¬p)∨q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,5) | B. | (-$\frac{1}{3}$,5) | C. | (-∞,5] | D. | [5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
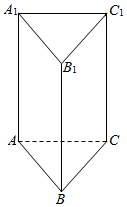 三棱柱ABC-A1B1C1中,底面ABC为等边三角形,AB=2,C1C⊥底面ABC,BC1与底面ABC所成角为45°,则此三棱柱体积是2$\sqrt{3}$.
三棱柱ABC-A1B1C1中,底面ABC为等边三角形,AB=2,C1C⊥底面ABC,BC1与底面ABC所成角为45°,则此三棱柱体积是2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com