
| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 4 |
分析 根据条件便可得出向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{3π}{4}$,然后可作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$,并连接AC,BC,这样由此可得到$∠AOB=\frac{3π}{4},∠ACB=\frac{π}{4}$,这便说明O,A,C,B四点共圆,从而当OC为圆的直径时$|\overrightarrow{c}|$最大.并且可以得到$\frac{\sqrt{2}}{cos∠AOC}=\frac{1}{cos(\frac{3π}{4}-∠AOC)}$,这样便可得出AC=$2\sqrt{2}$,从而在Rt△AOC中可以求出OC的值,这样即可得出$|\overrightarrow{c}|$的最大值.
解答 解:根据条件,$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>=\sqrt{2}cos<\overrightarrow{a},\overrightarrow{b}>=-1$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=-\frac{\sqrt{2}}{2}$;
∴向量$\overrightarrow{a},\overrightarrow{b}$夹角为$\frac{3π}{4}$;
如图,作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,连接AC,BC,则: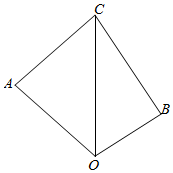
$\overrightarrow{CA}=\overrightarrow{a}-\overrightarrow{c},\overrightarrow{CB}=\overrightarrow{b}-\overrightarrow{c}$;
∴$∠ACB=\frac{π}{4}$;
又$∠AOB=\frac{3π}{4}$;
∴O,A,C,B四点共圆;
∴当OC为圆的直径时,$|\overrightarrow{c}|$最大;
∴此时$∠A=∠B=\frac{π}{2}$,$OA=\sqrt{2},OB=1$,$∠BOC=\frac{3π}{4}-∠AOC$;
∴$\frac{\sqrt{2}}{cos∠AOC}=\frac{1}{cos(\frac{3π}{4}-∠AOC)}$;
∴$cos∠AOC=\sqrt{2}(-\frac{\sqrt{2}}{2}cos∠AOC+\frac{\sqrt{2}}{2}sin∠AOC)$;
整理得2cos∠AOC=sin∠AOC;
∴tan∠AOC=2;
∴$AC=2\sqrt{2}$;
∴$OC=\sqrt{O{A}^{2}+A{C}^{2}}=\sqrt{10}$;
∴$|\overrightarrow{c}|=\sqrt{10}$;
即$|\overrightarrow{c}|$的最大值为$\sqrt{10}$.
故选:C.
点评 考查向量数量积的计算公式,向量夹角的概念及范围,向量减法的几何意义,圆的内接四边形的对角互补,直径所对的圆周角为直角,以及两角差的余弦公式,三角函数的定义,直角三角形边的关系.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5x-12y+38=0或3x-4y+10=0 | B. | 12x-5y+4=0或3x-4y+10=0 | ||
| C. | 5x-12y+38=0或x=2 | D. | 3x-4y+10=0或x=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{2}$ | B. | -$\frac{2}{5}$ | C. | $\frac{2}{5}$ | D. | $±\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22 | B. | 23 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 从匀速传递的产品生产流水线上,质检员每5分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样 | |
| B. | 已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有${x^{\frac{1}{2}}}<{x^{\frac{1}{3}}}$,则 p∨(¬q)是真命题 | |
| C. | “sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件 | |
| D. | 命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
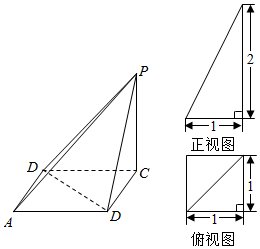
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com