
分析 设出点P(x,y),用直线AB的倾斜角α表示x、y,得出曲线C的参数方程
解答 解:设P(x,y),由题设知,直线AB的倾斜角为α,
∴x=$\frac{1}{3}$|AB|cos(π-α)=-2cosα,y=$\frac{2}{3}$|AB|sin(π-α)=$\frac{4}{3}$sinα,
∴点P的轨迹的参数方程是$\left\{\begin{array}{l}{x=-2cosα}\\{y=\frac{4}{3}sinα}\end{array}\right.$(α为参数,90°<α<180°).
故答案为:$\left\{\begin{array}{l}{x=-2cosα}\\{y=\frac{4}{3}sinα}\end{array}\right.$(α为参数,90°<α<180°).
点评 本题考查了轨迹方程,考查参数方程,考查学生的逻辑思维能力和计算能力,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | (0,2] | C. | (2,3) | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
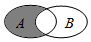 已知集合A={0,1,2,3,4,5},B={-3,-2,-1,0,1,2,3},则图中阴影部分表示的集合为( )
已知集合A={0,1,2,3,4,5},B={-3,-2,-1,0,1,2,3},则图中阴影部分表示的集合为( )| A. | {4,5} | B. | {4,5,6} | C. | {x|4≤x≤5} | D. | {x|4≤x≤6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某次数学小测验中(满分100分),某班50名学生得分如下面的频率分布直方图所示:
某次数学小测验中(满分100分),某班50名学生得分如下面的频率分布直方图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com