
| A. | g(x)的一条对称轴方程为x=$\frac{π}{12}$ | B. | g(x)的值域为[-$\sqrt{2}$,$\sqrt{2}$] | ||
| C. | 在(0,π)上单调递减 | D. | 关于点($\frac{13π}{12}$,$\frac{1}{2}$)对称 |
分析 利用已知及函数y=Asin(ωx+φ)的图象变换可得g(x)=$\frac{\sqrt{2}}{2}$sin(x-$\frac{π}{12}$)+$\frac{1}{2}$,由x-$\frac{π}{12}$=kπ+$\frac{π}{2}$,k∈Z,解得g(x)的一条对称轴方程可判断A,由g(x)∈[$\frac{1}{2}$-$\frac{\sqrt{2}}{2}$,$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$],可判断B;由2kπ+$\frac{π}{2}$≤x-$\frac{π}{12}$≤2kπ+$\frac{3π}{2}$,k∈Z,解得g(x)的单调递减区间,可判断C;由x-$\frac{π}{12}$=kπ,k∈Z,解得g(x)的对称中心坐标,可判断D,从而得解.
解答 解:∵把函数f(x)=cos2x+sinxcosx=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)+$\frac{1}{2}$的图象向右平移$\frac{π}{6}$个单位长度,可得函数y=$\frac{\sqrt{2}}{2}$sin[2(x-$\frac{π}{6}$)+$\frac{π}{4}$]+$\frac{1}{2}$=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{12}$)+$\frac{1}{2}$的图象,
再把所得图象每个点的横坐标扩大为原来的2倍,得到函数g(x)=$\frac{\sqrt{2}}{2}$sin(x-$\frac{π}{12}$)+$\frac{1}{2}$的图象,
∴由x-$\frac{π}{12}$=kπ+$\frac{π}{2}$,k∈Z,解得g(x)的一条对称轴方程为:x=kπ+$\frac{7π}{12}$,k∈Z,可得A错误;
由g(x)=$\frac{\sqrt{2}}{2}$sin(x-$\frac{π}{12}$)+$\frac{1}{2}$∈[$\frac{1}{2}$-$\frac{\sqrt{2}}{2}$,$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$],可得B错误;
由2kπ+$\frac{π}{2}$≤x-$\frac{π}{12}$≤2kπ+$\frac{3π}{2}$,k∈Z,解得g(x)的单调递减区间为:[2kπ+$\frac{7π}{12}$,2kπ+$\frac{19π}{12}$],k∈Z,可得C错误;
由x-$\frac{π}{12}$=kπ,k∈Z,解得g(x)的对称中心坐标为:(kπ+$\frac{π}{12}$,$\frac{1}{2}$),k∈Z,当k=1时,为($\frac{13π}{12}$,$\frac{1}{2}$),可得D正确.
故选:D.
点评 本题主要考查了三角函数恒等变换的应用,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质的综合应用,考查了转化思想和数形结合思想,属于基础题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
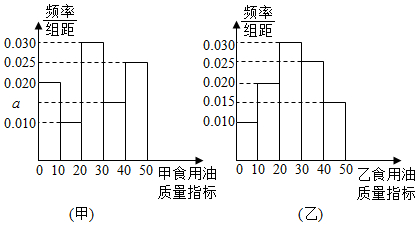
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若“p∨q”为假命题,则p,q均为假命题 | |
| B. | “a>b”是“ac2>bc2”的充分不必要条件 | |
| C. | 命题:“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0” | |
| D. | 命题:“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在这四个数中至少存在两个数x,y,满足sin(x-y)>$\frac{1}{2}$ | |
| B. | 在这四个数中至少存在两个数x,y,满足cos(x-y)≥$\frac{{\sqrt{3}}}{2}$ | |
| C. | 在四个数中至多存在两个数x,y,满足tan(x-y)<$\frac{{\sqrt{3}}}{3}$ | |
| D. | 在这四个数中至多存在两个数x,y,满足sin(x-y)≥$\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,5) | B. | (-$\frac{1}{3}$,5) | C. | (-∞,5] | D. | [5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
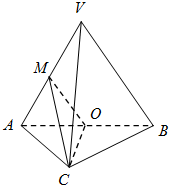 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com